题目内容
8.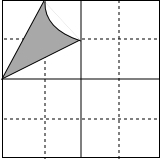 如图,已知网格中每个小正方形的边长为都是1,图中的阴影部分图案是一条以格点为圆心,以1为半径的圆弧和两条线段围成.
如图,已知网格中每个小正方形的边长为都是1,图中的阴影部分图案是一条以格点为圆心,以1为半径的圆弧和两条线段围成.(1)填空:图中阴影部分的面积是2-$\frac{1}{4}$π
(2)请你在网格中以阴影图案为基本图案,借助轴对称,平移或是旋转设计一个完整的图案.
分析 (1)从图中可以发现阴影部分的面积等于边长为2的正方形的面积减去两个底为2,高为1的三角形的面积和半径为1的扇形面积即可.
(2)先在右边作一个轴对称图形,再把两个图形分别旋转90度画出图形即可.
解答 解:(1)阴影部分的面积是2×2-2×$\frac{1}{2}$×2×1-$\frac{1}{4}$π×12=2-$\frac{1}{4}$π;
(2)作图如下:
点评 此题考查利用旋转、轴对称以及平移设计图案,组合面积的计算方法,掌握旋转、平移、轴对称的性质是解决问题的关键.

练习册系列答案
相关题目
13.矩形具有而菱形不具有的性质是( )
| A. | 对角线平分一组对角 | B. | 对角线相等 | ||
| C. | 对角线互相垂直 | D. | 四条边相等 |
18.某企业信息部进行市场调查发现:
信息一、如果单独投资A种产品,所投资利润yA(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表:
信息二:如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间存在二次函数关系:yB=ax2+bx,且投资2万元时获利润2.4万元,当投资4万元时,可获利润3.2万元.
(1)从所学过的函数中猜想yA与x之间的关系,并求出yA与x的函数关系式;
(2)求出yB与x的函数关系式,并求想利润yB为3(万元)应投资金额;
(3)如果企业同时对A、B两种产品共投资15万元,请设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?
信息一、如果单独投资A种产品,所投资利润yA(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表:
| x(万元) | 1 | 2 | 2.5 | 3 | 5 |
| yA(万元) | 0.4 | 0.8 | 1 | 1.2 | 2 |
(1)从所学过的函数中猜想yA与x之间的关系,并求出yA与x的函数关系式;
(2)求出yB与x的函数关系式,并求想利润yB为3(万元)应投资金额;
(3)如果企业同时对A、B两种产品共投资15万元,请设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?
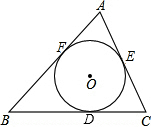 △ABC的内切圆⊙O的半径为3,点D、E、F为切点.△ABC的周长为18,求△ABC的面积.
△ABC的内切圆⊙O的半径为3,点D、E、F为切点.△ABC的周长为18,求△ABC的面积.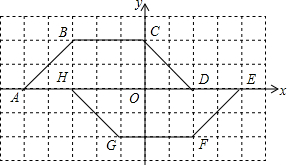 如图,网格平面直角坐标系中,组成网格的每个小正方形的边长为单位1.
如图,网格平面直角坐标系中,组成网格的每个小正方形的边长为单位1.