题目内容
6.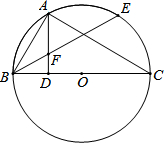 如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,$\widehat{AE}$=$\widehat{AB}$,BE交AD于点F.
如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,$\widehat{AE}$=$\widehat{AB}$,BE交AD于点F.(1)∠ACB与∠BAD相等吗?为什么?
(2)判断△FAB的形状,并说明理由.
分析 (1)根据圆周角定理求出∠BAC=90°,根据三角形内角和定理和垂直求出∠ACB+∠ABC=90°,∠BAD+∠ABC=90°,即可得出答案;
(2)根据圆周角定理求出∠ACB=∠ABE,推出∠BAD=∠ABE,根据等腰三角形的判定得出即可.
解答 解:(1)∠ACB与∠BAD相等,
理由是:∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠ACB+∠ABC=90°,
∵AD⊥BC,
∴∠BAD+∠ABC=90°,
∴∠ACB=∠BAD;
(2)△FAB是等腰三角形,
理由是:∵$\widehat{AE}$=$\widehat{AB}$,
∴∠ACB=∠ABE,
∵∠ACB=∠BAD,
∴∠BAD=∠ABE,
∴AF=BF,
∴△FAB是等腰三角形.
点评 本题考查了等腰三角形的判定,三角形内角和定理,圆周角定理,圆心角、弧、弦之间的关系等知识点的应用,能求出∠ACB=∠BAD是解此题的关键,题目比较典型,综合性比较强.

练习册系列答案
相关题目
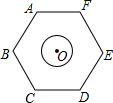 如图,圆心O恰好为正六边形ABCDEF的中心,已知AB=2$\sqrt{3}$,⊙O的半径为1,现将⊙O在正六边形内部沿某一方向平移,当它与正六边形ABCDEF的某条边相切时停止平移,设此时平移的距离为d,则d的取值范围是2≤d≤$\frac{4\sqrt{3}}{3}$.
如图,圆心O恰好为正六边形ABCDEF的中心,已知AB=2$\sqrt{3}$,⊙O的半径为1,现将⊙O在正六边形内部沿某一方向平移,当它与正六边形ABCDEF的某条边相切时停止平移,设此时平移的距离为d,则d的取值范围是2≤d≤$\frac{4\sqrt{3}}{3}$. 如图,C为⊙O的劣弧AB上一点,若∠AOB=124°,则∠ACB=118°.
如图,C为⊙O的劣弧AB上一点,若∠AOB=124°,则∠ACB=118°.
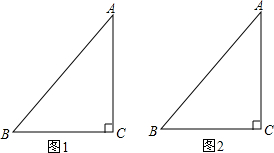 已知△ABC,∠C=90°,AC=4,BC=3.
已知△ABC,∠C=90°,AC=4,BC=3.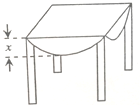 用一块直径为4米的圆桌布平铺在对角线长为4米的正方形桌面上(如示意图),若四周下垂的最大长度相等,则这个最大长度x为0.6米($\sqrt{2}$取1.4).
用一块直径为4米的圆桌布平铺在对角线长为4米的正方形桌面上(如示意图),若四周下垂的最大长度相等,则这个最大长度x为0.6米($\sqrt{2}$取1.4).