题目内容
15.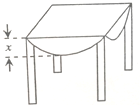 用一块直径为4米的圆桌布平铺在对角线长为4米的正方形桌面上(如示意图),若四周下垂的最大长度相等,则这个最大长度x为0.6米($\sqrt{2}$取1.4).
用一块直径为4米的圆桌布平铺在对角线长为4米的正方形桌面上(如示意图),若四周下垂的最大长度相等,则这个最大长度x为0.6米($\sqrt{2}$取1.4).
分析 画出平面图,连接OA,作OM⊥AB,垂足为N,交⊙O于M,由正方形的性质得出MN=x,ON=AN=$\frac{\sqrt{2}}{2}$OA=$\sqrt{2}$,得出x=OM-ON,即可得出结果.
解答 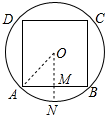 解:平面图如图所示:
解:平面图如图所示:
连接OA,作OM⊥AB,垂足为N,交⊙O于M,
则MN=x,OM=AM=$\frac{\sqrt{2}}{2}$OA=$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$,
∴x=OM-ON=2-$\sqrt{2}$≈0.6(米).
故答案为:0.6米.
点评 本题考查了正多边形和圆的位置关系、正方形的性质;熟练掌握正方形的性质,画出图形,由正方形的性质求出ON是解决问题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
20.下列说法中正确的选项是( )
| A. | 温度由-3℃上升3℃后达到-6℃ | |
| B. | 零减去一个数得这个数的相反数 | |
| C. | $\frac{π}{3}$既是分数,又是有理数 | |
| D. | 20.12既不是整数,也不是分数,所以它不是有理数 |
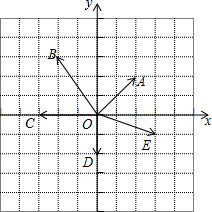 如图,在单位正方形网格中,建立直角坐标系,设$\overrightarrow{i}$、$\overrightarrow{j}$分别是x轴、y轴上的单位向量,试用$\overrightarrow{i}$、$\overrightarrow{j}$的线性组合表示下列在图中标出的向量.(直接将结果填在横线上)
如图,在单位正方形网格中,建立直角坐标系,设$\overrightarrow{i}$、$\overrightarrow{j}$分别是x轴、y轴上的单位向量,试用$\overrightarrow{i}$、$\overrightarrow{j}$的线性组合表示下列在图中标出的向量.(直接将结果填在横线上) 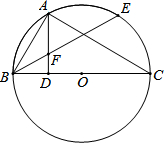 如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,$\widehat{AE}$=$\widehat{AB}$,BE交AD于点F.
如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,$\widehat{AE}$=$\widehat{AB}$,BE交AD于点F.