题目内容
15. 如图,有一张直角三角形纸片,两直角边AC=7cm,BC=11cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为$\frac{36}{11}$cm.
如图,有一张直角三角形纸片,两直角边AC=7cm,BC=11cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为$\frac{36}{11}$cm.
分析 根据翻折变换的性质可得AD=BD,设CD=x,表示出AD,然后在Rt△ACD中,利用勾股定理列方程求解即可.
解答 解:∵△ABC折叠,点B与点A重合,折痕为DE,
∴AD=BD,
设CD=x,则AD=BD=BC-CD=11-x,
在Rt△ACD中,根据勾股定理得,AC2+CD2=AD2,
即72+x2=(11-x)2,
解得x=$\frac{36}{11}$,
所以,CD的长为$\frac{36}{11}$cm.
故答案为:$\frac{36}{11}$cm.
点评 本题考查了翻折变换,主要利用了翻折前后对应边相等,此类题目,难点在于利用勾股定理列出方程.

练习册系列答案
相关题目
8.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成如下表:
(1)根据上表的数据,请你写出Q与t的关系式;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加满48L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
| 汽车行驶时间t/h | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q/L | 100 | 94 | 88 | 82 | … |
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加满48L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
10.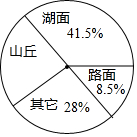 下面是我去某公园占地分布情况统计图:
下面是我去某公园占地分布情况统计图:
(1)湖面占地面积最大,路面占地面积最小.
(2)山丘占公园的22%.
(3)假设公园占地1200公顷,请填写下表.
 下面是我去某公园占地分布情况统计图:
下面是我去某公园占地分布情况统计图:(1)湖面占地面积最大,路面占地面积最小.
(2)山丘占公园的22%.
(3)假设公园占地1200公顷,请填写下表.
| 占地类型 | 湖面 | 山丘 | 路面 | 其它 |
| 占地面积(公顷) | 498 | 264 | 102 | 336 |
20.下列大写正体英文字母为中心对称图形的是( )
| A. | E | B. | S | C. | M | D. | U |
4.为了解我市老年人的健康状况,下列抽样调查最合理的是( )
| A. | 在公园调查部分老年人的健康状况 | |
| B. | 在医院调查部分老年人的健康状况 | |
| C. | 利用户籍网调查部分老年人的健康状况 | |
| D. | 在周围邻居中调查部分老年人的健康状况 |
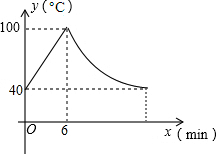 某型号的饮水机接通电源后就进入自动加热程序,水温升至100℃后自动停止加热,停止加热后水温开始下降,当水温降至40℃,饮水机再次启动自动加热,重复上述程序,一个周期内水温y(℃)与时间t(min)的关系如图所示,(水温上升过程中温度与时间成一次函数;水温下降过程中,温度与时间成反比例函数),根据图象,解答下列问题:
某型号的饮水机接通电源后就进入自动加热程序,水温升至100℃后自动停止加热,停止加热后水温开始下降,当水温降至40℃,饮水机再次启动自动加热,重复上述程序,一个周期内水温y(℃)与时间t(min)的关系如图所示,(水温上升过程中温度与时间成一次函数;水温下降过程中,温度与时间成反比例函数),根据图象,解答下列问题: