题目内容
把图1中的矩形ABCD折叠,B、C两点恰好重合,落在AD边上的点P处(如图2),已知:PM=3,PN=4,MN=5,则矩形面积为 .
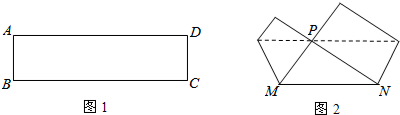

考点:翻折变换(折叠问题)
专题:
分析:根据折叠得出BM=PM=3,CN=PN=4,MN=5,求出BC,根据勾股定理求出MQ,求出PQ,根据面积公式求出即可.
解答:解: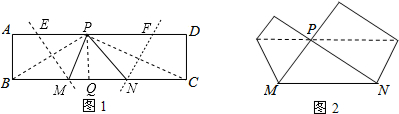
如图1,∵根据折叠的性质得:BM=PM=3,CN=PN=4,MN=5,
∴BC=3+4+5=12,
过P作PQ⊥BC于Q,则AB=DC=PQ,
在Rt△PQM和Rt△PQN中,由勾股定理得:PQ2=PM2-MQ2=PN2-NQ2,
即32-MQ2=42-(5-MQ)2,
解得:MQ=1.8,
则PQ=
=2.4,
∴AB=2.4,
∴矩形面积为2.4×12=28.8,
故答案为:28.8.

如图1,∵根据折叠的性质得:BM=PM=3,CN=PN=4,MN=5,
∴BC=3+4+5=12,
过P作PQ⊥BC于Q,则AB=DC=PQ,
在Rt△PQM和Rt△PQN中,由勾股定理得:PQ2=PM2-MQ2=PN2-NQ2,
即32-MQ2=42-(5-MQ)2,
解得:MQ=1.8,
则PQ=
| 32-1.82 |
∴AB=2.4,
∴矩形面积为2.4×12=28.8,
故答案为:28.8.
点评:本题考查了折叠的性质,矩形性质,勾股定理的应用,关键是求出BC和AB的长.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
数轴是一条( )
| A、射线 | B、直线 |
| C、线段 | D、以上都是 |
已知半径为1cm和半径为3cm的两圆相交,则其圆心距可能是( )
| A、2cm | B、3.5cm |
| C、4cm | D、6cm |
下列函数:①y=-
x;②y=2x+1;③y=-
(x<0);④y=-x2+2x+3,其中y的值随x值增大而增大的函数有( )
| 1 |
| 3 |
| 2 |
| x |
| A、4个 | B、3个 | C、2个 | D、1个 |
 某新建住宅小区里,有一块三角形绿地,现准备在其中安装一个照明灯P,使它到绿地各边的距离相等.请你在图中画出安装照明灯P的位置.
某新建住宅小区里,有一块三角形绿地,现准备在其中安装一个照明灯P,使它到绿地各边的距离相等.请你在图中画出安装照明灯P的位置.