题目内容
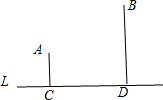如图，点A、B在直线L同侧，到L的垂线段AC=1cm，BD=3cm，CD=3cm．如果点P在L上运动，那么点P在什么位置时，线段PA与PB的和最短？PA+PB的最小值是多少？考点：轴对称-最短路线问题
专题：
分析：作点A关于直线L的对称点A′，连接A′B交直线L于点P，过点A′作直线AE⊥BD的延长线于点E，再根据勾股定理求出A′B的长即可．
解答：
解：作点A关于直线L的对称点A′，连接A′B交直线L于点P，
则点P即为所求点．
过点A′作直线AE⊥BD的延长线于点E，则线段A′B的长即为PA+PB的最小值．
∵AC=1cm，BD=3cm，CD=3cm，
∴A′C=1cm，BE=3+1=4cm，A′E=CD=3cm，
∴A′B=
=
=5（cm）．
答：PA+PB的最小值是5cm．
解：作点A关于直线L的对称点A′，连接A′B交直线L于点P，则点P即为所求点．
过点A′作直线AE⊥BD的延长线于点E，则线段A′B的长即为PA+PB的最小值．
∵AC=1cm，BD=3cm，CD=3cm，
∴A′C=1cm，BE=3+1=4cm，A′E=CD=3cm，
∴A′B=
| A′E2+BE2 |
| 32+42 |
答：PA+PB的最小值是5cm．
点评：本题考查的是轴对称-最短路线问题，熟知两点之间，线段最短是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，△ABC中，AB=AC=12，AB的垂直平分线分别交AC、AB于D、E．△ABD的周长等于27，求CD的长．
如图，E是边长为1的正方形ABCD中CD边上的一点，CD=x2-4x+1=（ ）
| A、（x-2）2+3 |
| B、（x-2）2-3 |
| C、（x+2）2+3 |
| D、（x+2）2-3 |