题目内容
 如图,E是边长为1的正方形ABCD中CD边上的一点,CD=
如图,E是边长为1的正方形ABCD中CD边上的一点,CD=| 3 |
考点:旋转的性质
专题:
分析:由四边形ABCD为正方形,得到AD=AB,∠DAB=90°,又△ADE绕点A顺时针旋转后与△ABF重合,则∠DAE等于∠BAF,根据CD=
DE,可得tan∠DAE=
,即可得到∠FAB的角度.
| 3 |
| DE |
| AD |
解答:解:∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90°,
又∵△ADE绕点A顺时针旋转后与△ABF重合,
∴∠DAB=∠EAF=90°,
∵CD=
DE,
∴tan∠DAE=
=
=
,
∴∠DAE=30°,
∴∠FAB=30°.
故答案为:30°.
∴AD=AB,∠DAB=90°,
又∵△ADE绕点A顺时针旋转后与△ABF重合,
∴∠DAB=∠EAF=90°,
∵CD=
| 3 |
∴tan∠DAE=
| DE |
| AD |
| 1 | ||
|
| ||
| 3 |
∴∠DAE=30°,
∴∠FAB=30°.
故答案为:30°.
点评:本题考查了旋转的性质以及三角函数:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了正方形的性质.

练习册系列答案
相关题目
下列说法正确的是( )
| A、一个有理数不是正数就是负数 |
| B、符号不同的两个数是互为相反数 |
| C、任何一个有理数都有相反数 |
| D、零是最小的正整数 |
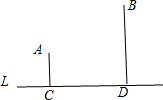 如图,点A、B在直线L同侧,到L的垂线段AC=1cm,BD=3cm,CD=3cm.如果点P在L上运动,那么点P在什么位置时,线段PA与PB的和最短?PA+PB的最小值是多少?
如图,点A、B在直线L同侧,到L的垂线段AC=1cm,BD=3cm,CD=3cm.如果点P在L上运动,那么点P在什么位置时,线段PA与PB的和最短?PA+PB的最小值是多少? 把下列各数所表示的点画在数轴上,再按从大到小的顺序用“>”号把这些数连结起来:-5,0,-|-3|,-(-2),1.
把下列各数所表示的点画在数轴上,再按从大到小的顺序用“>”号把这些数连结起来:-5,0,-|-3|,-(-2),1. 实数a、b、c在数轴上的位置如图所示,化简
实数a、b、c在数轴上的位置如图所示,化简