题目内容
若关于x的一元二次方程x2+2（m-3）x+m2=2有两个不相等的实数根x1、x2，且两根的绝对值是Rt△ABC两直角边的长，斜边长为4
，求|
|+|
|的值．
| 6 |
| x1 |
| x2 |
| x2 |
| x1 |
考点：根与系数的关系,根的判别式,勾股定理
专题：
分析：根据根与系数的关系，可得x1+x2=6-2m；x1x2=m2-2，根据勾股定理，可得x₁2+x₂2=96，根据解方程，可得m的值，根据解一元二次方程，可得方程的两个解，根据代入求值，可得答案．
解答：解：∵有两个不相等的实数根，
∴△=4（m-3）2-4（m2-2）=-24m+44＞0，解得m＜
；
由根与系数的关系，得
x1+x2=-2（m-3）=6-2m；x1x2=m2-2，
x₁2+x₂2=（x₁+x₂）2-2x₁x₂=4（3-m）2-2（m2-2）=-24m+40=96，解得m=-14，
关于x的一元二次方程x2+2（m-3）x+m2=2是x2-34x+194=0，
解得x1=17+
，x2=17-
，
|
|+|
|=|
|+|
|
=
+
=
．
∴△=4（m-3）2-4（m2-2）=-24m+44＞0，解得m＜
| 11 |
| 6 |
由根与系数的关系，得
x1+x2=-2（m-3）=6-2m；x1x2=m2-2，
x₁2+x₂2=（x₁+x₂）2-2x₁x₂=4（3-m）2-2（m2-2）=-24m+40=96，解得m=-14，
关于x的一元二次方程x2+2（m-3）x+m2=2是x2-34x+194=0，
解得x1=17+
| 95 |
| 95 |
|
| x1 |
| x2 |
| x2 |
| x1 |
17+
| ||
17-
|
17-
| ||
17+
|
=
384+2
| ||
| 194 |
384-2
| ||
| 194 |
=
| 384 |
| 97 |
点评：本题考查了根与系数的关系，利用了根与系数的关系，勾股定理，解一元二次方程．
练习册系列答案
相关题目
小利家距学校5千米，小兰家距学校10千米，小利家与小兰家的距离是x千米，则x的取值范围是（ ）
| A、x≥5 | B、x≤15 |
| C、5＜x＜15 | D、5≤x≤15 |
如图，反比例函数的图象与二次函数y=-x2+bx+c的图象在第一象限内相交于A，B两点，A，B两点的纵坐标分别为1，3，且AB=2下列说法正确的是（ ）
| A、一个有理数不是正数就是负数 |
| B、符号不同的两个数是互为相反数 |
| C、任何一个有理数都有相反数 |
| D、零是最小的正整数 |
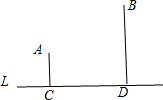如图，点A、B在直线L同侧，到L的垂线段AC=1cm，BD=3cm，CD=3cm．如果点P在L上运动，那么点P在什么位置时，线段PA与PB的和最短？PA+PB的最小值是多少？