题目内容
10.一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得是白球的概率与不是白球的概率相同,那么m与n的关系是( )| A. | m+n=4 | B. | m+n=8 | C. | m=n=4 | D. | m=3,n=5 |
分析 由于每个球都有被摸到的可能性,故可利用概率公式求出摸到白球的概率与摸到的球不是白球的概率,列出等式,求出m、n的关系.
解答 解:根据概率公式,摸出白球的概率为:$\frac{8}{8+m+n}$,
摸出不是白球的概率为:$\frac{m+n}{8+m+n}$,
由于二者相同,故有$\frac{8}{8+m+n}$=$\frac{m+n}{8+m+n}$,
整理得,m+n=8.
故选:B.
点评 此题考查概率公式,掌握概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{n}{m}$是解题的关键.

练习册系列答案
相关题目
1.下列计算正确的是( )
| A. | a+2a=3a2 | B. | (-a3)2=a6 | C. | a3•a2=a6 | D. | a8÷a4=a2 |
18.2017的倒数是( )
| A. | $\frac{1}{2017}$ | B. | -$\frac{1}{2017}$ | C. | 2017 | D. | -2017 |
5.在公式S=$\frac{1}{2}$ah中,已知a、h都是正数,则根据等式性质变形正确的是( )
| A. | $\frac{1}{2}$S=ah | B. | 2S=ah | C. | S-h=$\frac{1}{2}$a | D. | $\frac{S}{2a}$=h |
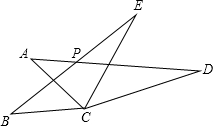 如图,△ACD与△BCE中,AC=BC,AD=BE,CD=CE,若∠ACE=80°,∠BCD=160°,AD与BE相交于P点,则∠ACB的度数为40°,∠APB的度数为40°.
如图,△ACD与△BCE中,AC=BC,AD=BE,CD=CE,若∠ACE=80°,∠BCD=160°,AD与BE相交于P点,则∠ACB的度数为40°,∠APB的度数为40°.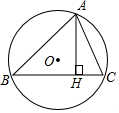 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=20,AH=16,⊙O的半径为15,则AB=24.
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=20,AH=16,⊙O的半径为15,则AB=24.