题目内容
2.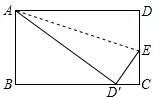 在长方形纸片ABCD中,AB=8,AD=10,将这张纸片沿AE折叠,使点D与点D′重合,D′在线段BC上,则AE的长为$\sqrt{89}$.
在长方形纸片ABCD中,AB=8,AD=10,将这张纸片沿AE折叠,使点D与点D′重合,D′在线段BC上,则AE的长为$\sqrt{89}$.
分析 由长方形ABCD沿AE折叠后,D点恰与BC边上的D′重合,可得AD′=AD=10,DE=ED′,然后设EC=x,则DE=ED′=CD-EC=8-x,首先在Rt△ABD′中,利用勾股定理求得BD′的长,继而可求得CD′的长,然后在Rt△CED′中,由勾股定理即可求得方程:x2+42=(8-x)2,求出x的长,进而得出DE的长,利用勾股定理即可得出结论.
解答 解:∵四边形ABCD是长方形,
∴∠B=∠C=90°,AD=BC=10,CD=AB=8,
∵△ADE折叠后得到△AD′E,
∴AD′=AD=10,DE=ED′,
设EC=x,则DE=ED′=CD-EC=8-x,
∵在Rt△ABF中,AB2+BD′2=AD′2,
∴82+BD′2=102,
∴BD′=6,
∴CF=BC-BD′=10-6=4,
∵在Rt△EFC中,EC2+CD′2=ED′2,
∴x2+42=(8-x)2,
解得,x=3,则DE=8-3=5,
在Rt△ADE中,AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{8}^{2}+{5}^{2}}$=$\sqrt{89}$.
故答案为:$\sqrt{89}$.
点评 本题考查的是翻折变换,熟知图形翻折不变性的性质及勾股定理是解答此题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
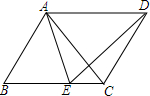 如图,在四边形ABCD中,AD∥BC,AD=BC,E为BC边上一点,且AB=AE.(1)求证:△ABC≌△EAD;
如图,在四边形ABCD中,AD∥BC,AD=BC,E为BC边上一点,且AB=AE.(1)求证:△ABC≌△EAD; 小华和小红都从同一点O出发,当小华向正北走了80米到A点,小红向正东走到B点时,两人相距为170米,则小红向正东方向走了多少米?
小华和小红都从同一点O出发,当小华向正北走了80米到A点,小红向正东走到B点时,两人相距为170米,则小红向正东方向走了多少米?