题目内容
7.已知$\frac{1}{x}$+$\frac{1}{y}$=$\frac{3}{x+y}$,则$\frac{y}{x}$+$\frac{x}{y}$=1.分析 由$\frac{1}{x}$+$\frac{1}{y}$=$\frac{3}{x+y}$,可得xy(x+y)≠0,根据等式的性质,等式两边同乘xy(x+y),得y(x+y)+x(x+y)=3xy,整理,得x2+y2=xy,再将$\frac{y}{x}$+$\frac{x}{y}$通分得到$\frac{{x}^{2}+{y}^{2}}{xy}$,然后代入即可.
解答 解:∵$\frac{1}{x}$+$\frac{1}{y}$=$\frac{3}{x+y}$,
∴xy(x+y)≠0,两边同乘xy(x+y),
得y(x+y)+x(x+y)=3xy,
整理,得x2+y2=xy,
∴$\frac{y}{x}$+$\frac{x}{y}$=$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{xy}{xy}$=1.
故答案为1.
点评 本题考查了比例的性质,等式的性质,分式的计算,将已知等式变形得出x2+y2=xy是解题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
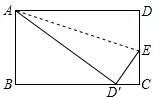 在长方形纸片ABCD中,AB=8,AD=10,将这张纸片沿AE折叠,使点D与点D′重合,D′在线段BC上,则AE的长为$\sqrt{89}$.
在长方形纸片ABCD中,AB=8,AD=10,将这张纸片沿AE折叠,使点D与点D′重合,D′在线段BC上,则AE的长为$\sqrt{89}$.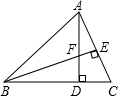 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE相交于点F,若BF=AC,求证:BD=AD.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE相交于点F,若BF=AC,求证:BD=AD.