题目内容
10.如图,点A,B是在数轴上对应的数字分别为-12和4,动点P和Q分别从A,B两点同时出发向右运动,点P的速度是5个单位/秒,点Q的速度是2个单位/秒.设运动时间为t秒.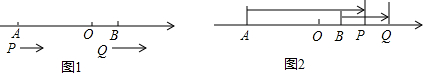
(1)AB=16.
(2)当点P在线段BQ上时(如图):
①BP=5t-16(用含t的代数式表示);②当P点为BQ中点时,求t的值.
(3)在运动过程中,当OP=2OQ时,点Q在数轴上所对应的数为多少?
分析 (1)根据数轴上两点间的距离公式结合A、B两点表示的数,即可得出结论;
(2)①根据“路程=速度×时间”“表示出来线段AP的长,再根据线段之间的关系即可得出结论;
②根据“路程=速度×时间”“表示出来线段BQ的长,再结合①的结论即可得出关于时间t的一元一次方程,解方程即可得出结论;
(3)分两种情况:
①当P在线段OA上时,如图3,②当P在点Q的右侧时,如图4,分别根据OP=2OQ列方程,求出对应t的值,再计算OQ的长,就可以得出结论.
解答 解:(1)∵点A,B是在数轴上对应的数字分别为-12和4,
∴AB=4-(-12)=16.
故答案为:16.
(2)如图2,①∵点P从点A出发向右以5个单位/秒的速度运动,
∴AP=5t,
∵AP=AB+BP,且AB=16,
∴BP=AP-AB=5t-16.
故答案为:5t-16.
②∵点Q从点B出发向右以2个单位/秒的速度运动,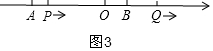
∴BQ=2t,
∵P点为BQ中点,且BP=5t-16,
∴2t=2×(5t-16),
解得:t=4.
故当P点为BQ中点时,t的值为4;
(3)分两种情况:
①当P在线段OA上时,如图3,
AP=5t,BQ=2t,则OP=OA-AP=12-5t,OQ=OB+BQ=4+2t,
∵OP=2OQ,
∴12-5t=2(4+2t),
t=$\frac{4}{9}$,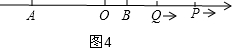
则OQ=4+2×$\frac{4}{9}$=4$\frac{8}{9}$,
②当P在点Q的右侧时,如图4,
此时OP=AP-OA=5t-12,OQ=4+2t,
∵OP=2OQ,
∴5t-12=2(4+2t),
t=20,
∴OQ=4+2×20=44,
答:当OP=2OQ时,点Q在数轴上所对应的数为4$\frac{8}{9}$或44.
点评 本题考查了一元一次方程的应用以及数轴上两点间的距离公式,解题的关键是:(1)根据两点间的距离公式求出线段AB的长;(2)①根据数量关系表示出AP的长度;②根据数量关系表示出BQ的长度.本题属于基础题,难度不大,解决该题型题目时,结合数量关系表示出线段的长度,再根据线段间的关系列出方程是关键.


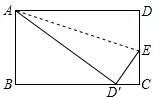 在长方形纸片ABCD中,AB=8,AD=10,将这张纸片沿AE折叠,使点D与点D′重合,D′在线段BC上,则AE的长为$\sqrt{89}$.
在长方形纸片ABCD中,AB=8,AD=10,将这张纸片沿AE折叠,使点D与点D′重合,D′在线段BC上,则AE的长为$\sqrt{89}$. 如图所示,直线a∥b,∠1=130°,∠2=70°,求∠3的度数.
如图所示,直线a∥b,∠1=130°,∠2=70°,求∠3的度数.