题目内容
 如图,将一张长方形纸片沿EF折叠后,点D、C分别落在点D′、C′的位置,ED′的延长线与BC相交于点G,若∠EFG=50°,则∠1=
如图,将一张长方形纸片沿EF折叠后,点D、C分别落在点D′、C′的位置,ED′的延长线与BC相交于点G,若∠EFG=50°,则∠1=考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:先根据平行线的性质得∠DEF=∠EFG=50°,∠1=∠GED,再根据折叠的性质得∠DEF=∠GEF=50°,则∠GED=100°,所以∠1=100°
解答:解:∵DE∥GC,
∴∠DEF=∠EFG=50°,∠1=∠GED,
∵长方形纸片沿EF折叠后,点D、C分别落在点D′、C′的位置,
∴∠DEF=∠GEF=50°,
即∠GED=100°,
∴∠1=∠GED=100°.
故答案为:100.
∴∠DEF=∠EFG=50°,∠1=∠GED,
∵长方形纸片沿EF折叠后,点D、C分别落在点D′、C′的位置,
∴∠DEF=∠GEF=50°,
即∠GED=100°,
∴∠1=∠GED=100°.
故答案为:100.
点评:本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了折叠的性质.

练习册系列答案
相关题目
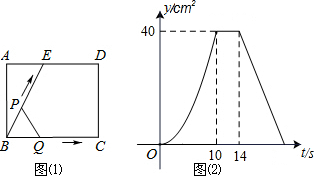 如图(1),E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是( )
如图(1),E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是( )| A、AE=8 | ||
B、当0≤t≤10时,y=
| ||
C、sin∠EBD=
| ||
| D、当t=12s时,△BPQ是等腰三角形 |
 如图,矩形ABCD的对角线AC和BD相交于点O,OA的垂直平分线BE恰好经过矩形的顶点B,求∠BAO的度数.
如图,矩形ABCD的对角线AC和BD相交于点O,OA的垂直平分线BE恰好经过矩形的顶点B,求∠BAO的度数. 如图,某双曲线上三点A、B、C的横坐标分别为1、2、3.若AB=2BC,则该双曲线的解析式为y=
如图,某双曲线上三点A、B、C的横坐标分别为1、2、3.若AB=2BC,则该双曲线的解析式为y= 已知:如图,有一块边长为8m正方形的土地,上面修了横纵各两条路,宽度都是1m,空白部分种上各种花草,则种花草的面积
已知:如图,有一块边长为8m正方形的土地,上面修了横纵各两条路,宽度都是1m,空白部分种上各种花草,则种花草的面积