Question

1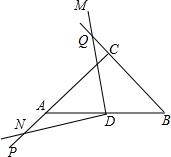．在△ABC中，∠A=∠B=α，点D为AB中点，∠MDN=2α，当∠MDN绕点D旋转的过程中，DN交AC于点P，DM交BC于点Q，探究DP，DQ的数量关系，并证明．

Answer 1

分析 连接PQ、CD；由三角形的外角性质和已知条件得出∠QCP=∠MON，证出P、Q、C、D四点共圆，由圆周角定理得出∠PQD=∠PCD，由圆内接四边形的性质得出∠BCD=∠DPQ，证出AC=BC，由等腰三角形的性质得出∠PCD=∠BCD，证出∠PQD=∠DPQ，即可得出结论．

解答 解：DP=DQ；理由如下：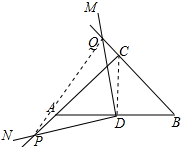
连接PQ、CD；如图所示：
∵∠QCP=∠CAB+∠B=2α，∠MDN=2α，
∴∠QCP=∠MDN，
∴P、Q、C、D四点共圆，
∴∠PQD=∠PCD，∠BCD=∠DPQ，
∵∠CAB=∠B，
∴AC=BC，
∵点D为AB中点，
∴CD平分∠ACB，
∴∠PCD=∠BCD，
∴∠PQD=∠DPQ，
∴DP=DQ．

点评 本题考查了四点共圆、圆周角定理、等腰三角形的判定与性质、圆内接四边形的性质；熟练掌握等腰三角形的性质，通过作辅助线证明四点共圆得出角相等是解决问题的关键．