题目内容
18. 如图所示,在一场足球赛中,一球员从球门正前方10m处将球踢起射向球门,当球飞行的水平距离是6m时,球达到最高点,此时球高3m,将球的运行路线看成是一条抛物线,若球门高为2.44m,则该球员能射中球门(填“能”或“不能”).
如图所示,在一场足球赛中,一球员从球门正前方10m处将球踢起射向球门,当球飞行的水平距离是6m时,球达到最高点,此时球高3m,将球的运行路线看成是一条抛物线,若球门高为2.44m,则该球员能射中球门(填“能”或“不能”).
分析 首先建立直角坐标系,顶点为(6,3),起点为(0,0).设抛物线的解析式为y=a(x-6)2+3,求出a的值.再代入x的值后易求出y的值.
解答 解:如图,建立直角坐标系,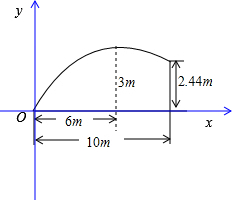
球飞行的路线为抛物线,顶点(6,3),起点(0,0),
设抛物线的解析式为y=a(x-6)2+3,
∴0=a(0-6)2+3,
∴a=-$\frac{1}{12}$;
∴抛物线的解析式为y=-$\frac{1}{12}$(x-6)2+3,
当x=10时,y=$\frac{5}{3}$<2.44,
故小王这一脚能射中球门,
故答案为:能.
点评 本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
10.已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如表所示:
点A(x1,y1)、B(x2,y2)在函数的图象上,则当0<x1<1,2<x2<3时,y1>y2.
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 4 | 1 | 0 | 1 | 4 | … |
8.若△ABC∽△DEF,△ABC与△DEF的相似比为1:3,则S△ABC:S△DEF为( )
| A. | 1:3 | B. | 1:9 | C. | 1:$\sqrt{3}$ | D. | 3:1 |
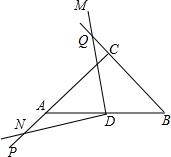 在△ABC中,∠A=∠B=α,点D为AB中点,∠MDN=2α,当∠MDN绕点D旋转的过程中,DN交AC于点P,DM交BC于点Q,探究DP,DQ的数量关系,并证明.
在△ABC中,∠A=∠B=α,点D为AB中点,∠MDN=2α,当∠MDN绕点D旋转的过程中,DN交AC于点P,DM交BC于点Q,探究DP,DQ的数量关系,并证明.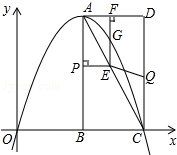 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.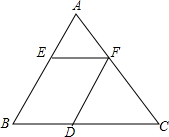 如图,△ABC中,EF∥BC,FD∥AB,AE=12,BE=18,AF=14,CD=24,求线段FC,EF的长.
如图,△ABC中,EF∥BC,FD∥AB,AE=12,BE=18,AF=14,CD=24,求线段FC,EF的长.