题目内容
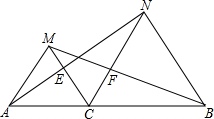 如图,点C为线段AB上一点△ACM、CBN是等边三角形.
如图,点C为线段AB上一点△ACM、CBN是等边三角形.求证:(1)AN=BM; (2)△ACE≌△MCF.
考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:(1)根据等边三角形的性质得出AC=CM,CN=CB,∠ACM=∠NCB=60°,求出∠ACN=∠MCB,根据SAS推出△ACN≌△MCB即可;
(2)根据△ACN≌△MCB得出∠CAE=∠CMF,求出∠MCF=∠ACM=60°,根据ASA推出即可.
(2)根据△ACN≌△MCB得出∠CAE=∠CMF,求出∠MCF=∠ACM=60°,根据ASA推出即可.
解答:证明:(1)∵△ACM、CBN是等边三角形,
∴AC=CM,CN=CB,∠ACM=∠NCB=60°,
∴∠ACB=∠MCB=60°+∠MCN,
在△ACN和△MCB中
∴△ACN≌△MCB,
∴AN=BM;
(2)∵△ACN≌△MCB,
∴∠CAE=∠CMF,
∵∠ACM=∠NCB=60°,
∴∠MCF=∠ACM=60°,
在△ACE和△MCF中
∴△ACE≌△MCF.
∴AC=CM,CN=CB,∠ACM=∠NCB=60°,
∴∠ACB=∠MCB=60°+∠MCN,
在△ACN和△MCB中
|
∴△ACN≌△MCB,
∴AN=BM;
(2)∵△ACN≌△MCB,
∴∠CAE=∠CMF,
∵∠ACM=∠NCB=60°,
∴∠MCF=∠ACM=60°,
在△ACE和△MCF中
|
∴△ACE≌△MCF.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,全等三角形的对应边相等,对应角相等.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
以下四个图中对称轴条数最多的一个图形是( )
A、 |
B、 |
C、 |
D、 |
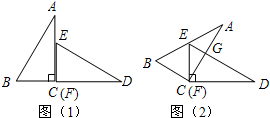 如图,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则BD之间的距离为
如图,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则BD之间的距离为 如图,已知AB∥DC,AD∥BC,求证:AB=CD.
如图,已知AB∥DC,AD∥BC,求证:AB=CD. 如图,已知:A、F、C、D四点在一条直线上,AF=CD,DE∥AB,且AB=DE.求证:EF∥CB.
如图,已知:A、F、C、D四点在一条直线上,AF=CD,DE∥AB,且AB=DE.求证:EF∥CB.