题目内容
已知整数k<5,若△ABC的边长均满足关于x的方程x2﹣3 x+8=0,则△ABC的周长是 .
x+8=0,则△ABC的周长是 .
6或12或10.
【解析】
试题分析:根据题意得k≥0且 ,而整数k<5,则k=4,方程变形为
,而整数k<5,则k=4,方程变形为 ,解得
,解得 ,所以△ABC的边长可以为2,2,2或4,4,4或4,4,2,则周长为6或12或10.
,所以△ABC的边长可以为2,2,2或4,4,4或4,4,2,则周长为6或12或10.
故答案为:6或12或10.
考点:一元二次方程的根的判别式;一元二次方程的解法;三角形的三边关系.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 ∥
∥ 的条件是( )
的条件是( )
 B.
B.
 D.
D.
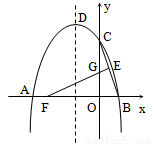
 (
( ≥0)与
≥0)与 (
( ≥0)的图象于B,C
≥0)的图象于B,C 的图象于点D,直线DE∥AC,交
的图象于点D,直线DE∥AC,交 的图象于点E,则
的图象于点E,则 .
.
 ,在数轴上表示解集并求出它的整数解的和.
,在数轴上表示解集并求出它的整数解的和. +(y+2)2=0,则yx= .
+(y+2)2=0,则yx= . 有意义,则x应满足( ).
有意义,则x应满足( ).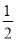 ≤x≤3 B.x≤3且x≠
≤x≤3 B.x≤3且x≠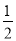 C.
C.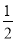 <x<3 D.
<x<3 D.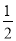 <x≤3
<x≤3 的整数解是___________.
的整数解是___________.