题目内容
(本题满分10分)某学校将周三“阳光体育”项目定为跳绳活动,为此学校准备购置长、短两种跳绳若干.已知长跳绳的单价比短跳绳单价的两倍多4元,且购买2条长跳绳与购买5条短跳绳的费用相同.
(1)两种跳绳的单价各是多少元?
(2)若学校准备用不超过2000元的现金购买200条长、短跳绳,且短跳绳的条数不超过长跳绳的6倍,问学校有几种购买方案可供选择?请说明哪种购买方案最省钱?
(1)长跳绳单价是20元,短跳绳的单价是8元;(2)共有5种购买方案可供选择;当 时,
时, 的值最小,即购买29条长跳绳与171条短跳绳最省钱.
的值最小,即购买29条长跳绳与171条短跳绳最省钱.
【解析】
试题分析:(1)设长跳绳的单价是x元,短跳绳的单价为y元,根据长跳绳的单价比短跳绳单价的两倍多4元,且购买2条长跳绳与购买5条短跳绳的费用相同分别列等式,联立方程组即可;
(2)设学校购买a条长跳绳,根据用不超过2000元的现金购买200条长、短跳绳,且短跳绳的条数不超过长跳绳的6倍,列不等式组即可确定有几种购买方案,进而确定最省钱的方案.
试题解析:【解析】
(1)设长跳绳的单价是x元,短跳绳的单价为y元.
由题意得: ,解得:
,解得: ,
,
所以长跳绳单价是20元,短跳绳的单价是8元.
(2)设学校购买a条长跳绳,
由题意得: ,解得:
,解得:  ,
,
∵a为正整数,∴a的整数值为29,30,31,32,33.
所以学校共有5种购买方案可供选择.当 时,
时, 的值最小,即购买29条长跳绳与171条短跳绳最省钱.
的值最小,即购买29条长跳绳与171条短跳绳最省钱.
考点:列方程组解应用题;列不等式组解应用题.
考点分析: 考点1:二元一次方程组 二元一次方程:如果一个方程含有两个未知数,并且所含未知项都为1次方,那么这个整式方程就叫做二元一次方程,有无穷个解,若加条件限定有有限个解。二元一次方程组,则一般有一个解,有时没有解,有时有无数个解。
二元一次方程的一般形式:ax+by+c=0其中a、b不为零。
二元一次方程的解:使二元一次方程左、右两边的值相等的一对未知数的值,叫做二元一次方程的一个解 。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 x+8=0,则△ABC的周长是 .
x+8=0,则△ABC的周长是 . B.
B. C.
C. D.
D.
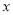 ,∠ACB=
,∠ACB= ,则
,则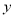 与
与 之间的关系是( ).
之间的关系是( ).
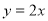 B.
B.
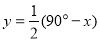 D.
D.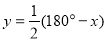


 ,则
,则 .
.