题目内容
(10分)解不等式组 ,在数轴上表示解集并求出它的整数解的和.
,在数轴上表示解集并求出它的整数解的和.
数轴见解析;-7.
【解析】
试题分析:分别解两个不等式,然后把解集表示在数轴上,进而求得x可取的整数,求这些整数的和.
试题解析:【解析】
解不等式①,得x<3,
解不等式②,得x≥﹣4.
在同一数轴上表示不等式①②的解集,得

∴这个不等式组的解集是﹣4≤x<3,
∴这个不等式组的整数解的和是﹣4﹣3﹣2﹣1+0+1+2=-7.
考点:不等式组的解法.
考点分析: 考点1:一元一次不等式一元一次不等式的定义:
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,这样的不等式叫做一元一次不等式。
注:
(1)首先要是一个不等式;
(2)不等式的两边都是整式;
(3)只含一个未知数,且未知数的最高次数是1。
一元一次不等式和一元一次方程概念的异同点:
相同点:二者都是只含有一个未知数,未知数的次数都是1,左、右两边都是整式.
不同点:一元一次不等式表示不等关系,一元一次方程表示相等关系.
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目

 为30m,从
为30m,从 点测得
点测得 点的俯角
点的俯角 为35°,测得
为35°,测得 点的俯角
点的俯角 为43°,求这两座建筑物的高度(结果保留小数点后1 位,参考数据
为43°,求这两座建筑物的高度(结果保留小数点后1 位,参考数据 ,
, ,
, ,
, ,
, ,
, ).
).
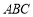 为⊙
为⊙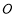 的内接三角形,
的内接三角形,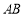 为⊙
为⊙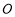 的直径,点
的直径,点 在⊙
在⊙ 上,
上, =55°,则
=55°,则 的大小等于( )
的大小等于( )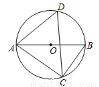
 .
.
 x+8=0,则△ABC的周长是 .
x+8=0,则△ABC的周长是 . cm B.
cm B. cm C.
cm C. cm D.
cm D. cm
cm