题目内容
18．
二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中错误的是（ ）| A． | a＜0 | B． | b＜0 | C． | c＞0 | D． | 图象过点（3，0） |
分析 根据函数的开口方向可以判断出a的正负，根据顶点在y轴右侧，可判断出a、b异号，根据与y轴的交点可判断出c的正负，根据对称轴和与x轴的一个交点可以得到另一个交点．
解答 解：由函数图象可知，
抛物线开口向下，可得a＜0，故选项A正确，
顶点在y轴右侧，在b＞0，故选项B错误，
抛物线与y轴交于正半轴，则c＞0，故选项C正确，
对称轴为直线x=1，与x轴的一个交点为（-1，0），则另一个交点是（3，0），故选项D正确．
故选B．
点评 本题考查二次函数图象与系数之间的关系，解题的关键是明确它们之间的关系，利用数形结合的思想进行解答．
练习册系列答案
53随堂测系列答案
相关题目
如图，在平面直角坐标系中，已知两点A（1，2），B（-1，-1），
9．直线l外一点P与直线l上两点的连线段长分别为3cm，5cm，则点P到直线l的距离是（ ）
| A． | 不超过3cm | B． | 3cm | C． | 5cm | D． | 不少于5cm |
13．如果4a=5b（ab≠0），那么下列比例式变形正确的是（ ）
| A． | $\frac{5}{a}=\frac{4}{b}$ | B． | $\frac{a}{4}=\frac{b}{5}$ | C． | $\frac{a}{b}=\frac{4}{5}$ | D． | $\frac{4}{a}=\frac{b}{5}$ |
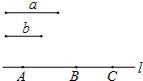尺规作图：如图，已知线段a，b．
如图，在等腰Rt△ABC和等腰Rt△ADE中，∠BAC=∠DAE=90°，点C、D、E在同一条直线上，连接BD，BE．以下四个结论：①BD=CE；②∠ACE+∠DBC=45°；③BD⊥CE；④BE2=2（AD2+AB2）．其中，结论正确的个数是（ ）
如图，在Rt△ABC中，∠C=90°，AC=12，BC=9，AB的垂直平分线分别交AB、AC于点D、E．求：
如图，在△ABC与△DCB中，已知∠ABD=∠DCE，∠DBC=∠ACB．