题目内容
3. 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )| A. | mn | B. | $\frac{1}{2}$mn | C. | $\frac{1}{4}$mn | D. | $\sqrt{mn}$ |
分析 连接OE,与DC交于点F,由四边形ABCD为矩形得到对角线互相平分且相等,进而得到OD=OC,再由两组对边分别平行的四边形为平行四边形得到ODEC为平行四边形,根据邻边相等的平行四边形为菱形得到四边形ODEC为菱形,得到对角线互相平分且垂直,求出菱形OCED的面积即可.
解答 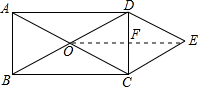 解:连接OE,与DC交于点F,
解:连接OE,与DC交于点F,
∵四边形ABCD为矩形,
∴OA=OC,OB=OD,且AC=BD,即OA=OB=OC=OD,
∵OD∥CE,OC∥DE,
∴四边形ODEC为平行四边形,
∵OD=OC,
∴四边形ODEC为菱形,
∴DF=CF,OF=EF,DC⊥OE,
∵DE∥OA,且DE=OA,
∴四边形ADEO为平行四边形,
∵AD=n,AB=m,
则S菱形ODEC=$\frac{1}{2}$OE•DC=$\frac{1}{2}$AB•AD=$\frac{1}{2}$mn.
故选B.
点评 此题考查了矩形的性质,菱形的判定与性质,以及勾股定理,熟练掌握矩形的性质是解本题的关键.

练习册系列答案
相关题目
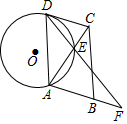 已知,如图,四边形ABCD是平行四边形,⊙O与边DC相切于点D,交对角线AC于点E,连接DE并延长交AB的延长线于点F,且AE=DE.
已知,如图,四边形ABCD是平行四边形,⊙O与边DC相切于点D,交对角线AC于点E,连接DE并延长交AB的延长线于点F,且AE=DE.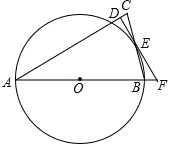 如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作O的切线交AC于点D,且ED⊥AC.
如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作O的切线交AC于点D,且ED⊥AC.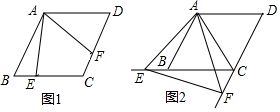
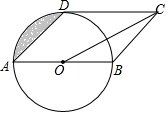 如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD相切于点D,若OC=2$\sqrt{5}$,则图中阴影部分的面积为π-2.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD相切于点D,若OC=2$\sqrt{5}$,则图中阴影部分的面积为π-2.