题目内容
18.已知P=$\frac{{n{m^2}+2m{n^2}+{n^3}-4m{n^2}}}{{m{{(m-n)}^2}}}$(m、n≠0,m≠n)(1)化简P;
(2)若点A(m,n)在正比例函数y=3x图象上,求P的值.
分析 (1)分子经过合并同类项、提取公因式后,可变形为n(m-n)2,结合m≠n即可得出P=$\frac{n}{m}$;
(2)由一次函数图象上点的坐标特征可得n=3m,结合(1)结论即可求出此时P=3.
解答 解:(1)P=$\frac{n{m}^{2}+2m{n}^{2}+{n}^{3}-4m{n}^{2}}{m(m-n)^{2}}$=$\frac{n{m}^{2}-2m{n}^{2}+{n}^{3}}{m(m-n)^{2}}$=$\frac{n({m}^{2}-2mn+{n}^{2})}{m(m-n)^{2}}$=$\frac{n(m-n)^{2}}{m(m-n)^{2}}$=$\frac{n}{m}$.
(2)∵点A(m,n)在正比例函数y=3x的图象上,
∴n=3m,
∴$\frac{n}{m}$=3,
∴P=$\frac{n}{m}$=3.
点评 本题考查了约分以及一次函数图象上点的坐标特征,解题的关键是:(1)将原分式化简为$\frac{n}{m}$;(2)根据一次函数图象上点的坐标特征找出n=3m.

练习册系列答案
相关题目
14. 直线a∥b,Rt△ABC的直角顶点C在直线a上,若∠1=35°,则∠2等于( )
直线a∥b,Rt△ABC的直角顶点C在直线a上,若∠1=35°,则∠2等于( )
 直线a∥b,Rt△ABC的直角顶点C在直线a上,若∠1=35°,则∠2等于( )
直线a∥b,Rt△ABC的直角顶点C在直线a上,若∠1=35°,则∠2等于( )| A. | 65° | B. | 50° | C. | 55° | D. | 60° |
3. 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )
 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )| A. | mn | B. | $\frac{1}{2}$mn | C. | $\frac{1}{4}$mn | D. | $\sqrt{mn}$ |
 把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ,$\frac{AB′}{AB}$=$\frac{B′C′}{BC}$=$\frac{AC′}{AC}$=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ=72°,n=$\frac{1+\sqrt{5}}{2}$.
把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ,$\frac{AB′}{AB}$=$\frac{B′C′}{BC}$=$\frac{AC′}{AC}$=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ=72°,n=$\frac{1+\sqrt{5}}{2}$.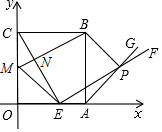 如图,边长为5的正方形OABC的顶点O在坐标原点处,点A,C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
如图,边长为5的正方形OABC的顶点O在坐标原点处,点A,C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.