题目内容
13.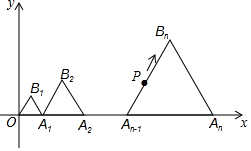 如图,在平面直角坐标系中,点A1,A2…,An都在x轴的正半轴上,OA1=1,A1A2=2,…An-1 An=n,分别以OA1,A1A2,…An-1 An为边,在x轴上方作等边三角形△OA1B1,△A1A2B2,…△An-1 AnBn,点B1,B2,…,Bn均落在第一象限,现有一动点P从点O出发,以每秒1个单位的速度沿折线O→B1→A1→B2→A2→…→Bn→An运动,则经2017秒后点P的坐标是(1008.5,$\frac{37\sqrt{3}}{2}$).
如图,在平面直角坐标系中,点A1,A2…,An都在x轴的正半轴上,OA1=1,A1A2=2,…An-1 An=n,分别以OA1,A1A2,…An-1 An为边,在x轴上方作等边三角形△OA1B1,△A1A2B2,…△An-1 AnBn,点B1,B2,…,Bn均落在第一象限,现有一动点P从点O出发,以每秒1个单位的速度沿折线O→B1→A1→B2→A2→…→Bn→An运动,则经2017秒后点P的坐标是(1008.5,$\frac{37\sqrt{3}}{2}$).
分析 先依次确定点A1、A2、A3、…、A44的坐标,此时离2017还差37秒,再从A44前进37秒即可,确定P所在边的位置,根据三角函数求值即可.
解答 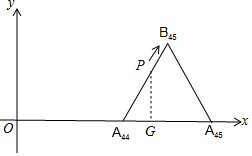 解:由题意得:
解:由题意得:
第1个三角形:边长为1,第1×2=2秒时,动点P落在A1(1,0);
第2个三角形,边长为2,第2×3=6秒时,动点P落在A2(3,0);
第3个三角形,边长为3,第3×4=12秒时,动点P落在A3(6,0);
…
第44个三角形,边长为44,第44×45=1980秒时,动点P落在A44(990,0);
2017-1980=37,
∴第2017秒时,点P落在边A44B45上,如图所示,
过P作PG⊥x轴于G,
∵∠PA44G=60°,
∴sin60°=$\frac{PG}{{A}_{44}P}$,
∴PG=37×$\frac{\sqrt{3}}{2}$=$\frac{37\sqrt{3}}{2}$,
同理得:A44G=$\frac{37}{2}$=18.5,
∴OG=990+18.5=1008.5,
∴P(1008.5,$\frac{37\sqrt{3}}{2}$),
故答案为:(1008.5,$\frac{37\sqrt{3}}{2}$).
点评 本题是有关点的坐标的规律题,根据图形选择一个比较好求的点的坐标,本题选择求一系数A点的坐标,因为此点在x轴上,其纵坐标为0,利用数形结合的思想解决问题,与特殊的三角函数相结合,使问题得以解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.一汽车的速度是每小时60千米,一次加满油可加40升,每小时耗油5升,t小时后行程S千米.
(1)写出一次加满油后所行路程S与时间t的函数关系式.
(2)求出自变量的取值范围.
(3)画出这个函数的图象.
(1)写出一次加满油后所行路程S与时间t的函数关系式.
(2)求出自变量的取值范围.
(3)画出这个函数的图象.
2.如果关于x的一元二次方程x2-6x+m=0有两个相等的实数根,则m所满足的条件是( )
| A. | m<9 | B. | m>9 | C. | m=9 | D. | m≤9 |
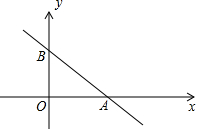 如图,直线y=-$\frac{3}{4}$x+3与坐标轴分别交于点A、B.
如图,直线y=-$\frac{3}{4}$x+3与坐标轴分别交于点A、B.