题目内容
3.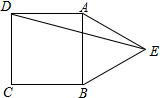 如图,等边△ABE与正方形ABCD有一条共公边,点E在正方形外,连结DE,则∠BED=45°.
如图,等边△ABE与正方形ABCD有一条共公边,点E在正方形外,连结DE,则∠BED=45°.
分析 根据正方形的性质,可得AB与AD的关系,∠BAD的度数,根据等边三角形的性质,可得AE与AB的关系,∠AEB的度数,根据等腰三角形的性质,可得∠AED与∠ADE的关系,根据三角形的内角和,可得∠AED的度数,根据角的和差,可得答案.
解答 解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵等边三角形ABE,
∴AB=AE,∠BAE=∠AEB=60°,
∠DAE=∠BAD+∠BAE=90°+60°=150°,
AD=AE,
∴∠AEB=∠ABE=(180°-∠DAB)÷2=15°,
∴∠BED=∠AEB-∠AED=60°-15°=45°,
故答案为:45°
点评 此题考查了正方形的性质,以及等边三角形的性质,利用了等量代换的思想,熟练掌握性质是解本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
18.在三边分别为下列长度的三角形中,不是直角三角形的为( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 2,3,$\sqrt{5}$ | C. | 5,13,12 | D. | 4,7,5 |
13.若△ABC三边分别是a、b、c,且满足(b-c)(a2+b2)=bc2-c3,则△ABC是( )
| A. | 等边三角形 | B. | 等腰三角形 | ||
| C. | 直角三角形 | D. | 等腰或直角三角形 |
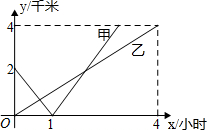 已知A、B、C是同一条笔直公路上的三个不同的车站,甲、乙两人分别从A、B车站同时出发,匀速直线运动到C站,到达C站就停下来,甲、乙两人与B站的距离y(千米)与时间x(小时)之间的函数关系的图象如图,当甲出发7小时,甲、乙两人相距5千米.
已知A、B、C是同一条笔直公路上的三个不同的车站,甲、乙两人分别从A、B车站同时出发,匀速直线运动到C站,到达C站就停下来,甲、乙两人与B站的距离y(千米)与时间x(小时)之间的函数关系的图象如图,当甲出发7小时,甲、乙两人相距5千米.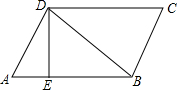 如图,?ABCD的周长为52cm,AB边的垂直平分线经过点D,垂足为E,?ABCD的周长比△ABD的周长多10cm.∠BDE=35°.
如图,?ABCD的周长为52cm,AB边的垂直平分线经过点D,垂足为E,?ABCD的周长比△ABD的周长多10cm.∠BDE=35°.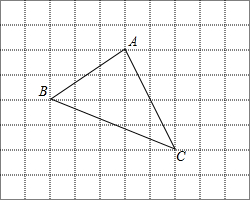 如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(-1,3),点C的坐标为(1,-1).
如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(-1,3),点C的坐标为(1,-1).