题目内容
7.为了观察植物的生长,校“水中花”社团准备购买A,B,C三种植物分别给同学们,每位同学只能选择三种植物中的一种,在对全社团的同学进行了全面调查后,得到如图所示的统计图:(1)根据如图所示统计图的信息,可知“水中花”社团一共有50名学生,扇形统计图中B所占的比例为36%;
(2)若在甲店购买A,B两种植物各1盆共需20元,购买1盆C植物需5元,按社团同学们喜欢的品种人数购买3个品种共需花费454元,则在甲店购买A,B两种植物的单价各是多少元?
(3)若在乙店购买A,B,C三种植物各1盆需花费24元,购买A,B,C三种植物分别为5,4,2盆共需94元,按社团同学们喜欢的品种人数购买3个品种共需花费424元.
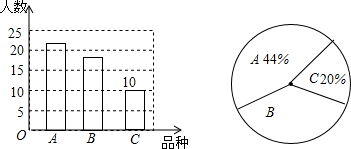
分析 (1)根据喜欢C种植物的人数及所占的百分比即可求出总人数,扇形统计图中B所占的比例为:100%-44%-20%=36%;
(2)先分别计算出喜欢A种植物的人数为:50×44%=22(人),喜欢B种植物的人数为:50×36%=18(人),设A种植物的单价是x元,则B种植物的单价为20-x元,根据题意得:22x+18(20-x)+10×5=454,即可解答;
(3)设A种植物x元一盆、B种植物y元一盆、C种植物z元一盆,由题意,得$\left\{\begin{array}{l}{x+y+z=24}\\{5x+4y+2z=94}\end{array}\right.$,再由这两个方程构成方程组,再解这个不定方程组求出其解即可.
解答 解:(1)“水中花”社团共有学生:10÷20%=50(人),扇形统计图中B所占的比例为:100%-44%-20%=36%.
故答案为:50,36;
(2)喜欢A种植物的人数为:50×44%=22(人),喜欢B种植物的人数为:50×36%=18(人),
设A种植物的单价是x元,则B种植物的单价为20-x元,
根据题意得:22x+18(20-x)+10×5=454,
解得:x=11.
20-11=9(元).
答:A种植物的单价是11元,则B种植物的单价为9元;
(3)设A种植物x元一盆、B种植物y元一盆、C种植物z元一盆,由题意,得
$\left\{\begin{array}{l}{x+y+z=24}\\{5x+4y+2z=94}\end{array}\right.$,
原方程组变形为:$\left\{\begin{array}{l}{2x+2y+2z=48①}\\{20a+16b+8c=376②}\end{array}\right.$
①+②得:22a+18b+10c=424.
答:按社团同学们喜欢的品种人数购买3个品种共需花费424元.
故答案为;424.
点评 本题主要考查了条形统计图,扇形统计图及用样本估计总体,解题的关键是读懂统计图,从统计图中获得准确的信息.

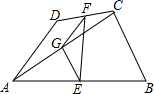 如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )
如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )| A. | 20° | B. | 24° | C. | 26° | D. | 15° |
| A. | -2 | B. | 1 | C. | -12 | D. | 12 |
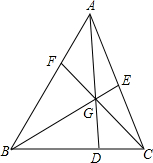 如图,在三角形ABC中,点D,E,F分别在BC,AC,AB上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,若S△BDG=8,S△AGE=3,求S△ABC.
如图,在三角形ABC中,点D,E,F分别在BC,AC,AB上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,若S△BDG=8,S△AGE=3,求S△ABC. 在△ABC中,AE为角平分线,AD为中线,CF⊥AE,AB=8,AC=6,求DF的长.
在△ABC中,AE为角平分线,AD为中线,CF⊥AE,AB=8,AC=6,求DF的长.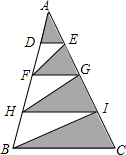 如图,三角形ABC中,将AB,AC分别四等分,已知三角形ADE的面积是6cm2,求阴影部分的面积.
如图,三角形ABC中,将AB,AC分别四等分,已知三角形ADE的面积是6cm2,求阴影部分的面积.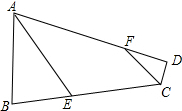 如图,在四边形ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,分别交BC,AD于点E,F.
如图,在四边形ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,分别交BC,AD于点E,F.