题目内容
11.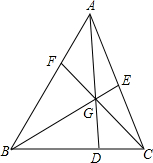 如图,在三角形ABC中,点D,E,F分别在BC,AC,AB上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,若S△BDG=8,S△AGE=3,求S△ABC.
如图,在三角形ABC中,点D,E,F分别在BC,AC,AB上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,若S△BDG=8,S△AGE=3,求S△ABC.
分析 首先根据两个三角形的高相同时,面积的比等于它们的底边的比,求出S△CGD,S△CGE的大小,进而求出S△BCE的大小;然后根据三角形的中线将三角形分成面积相等的两部分,用S△BCE的面积乘以2,求出△ABC的面积是多少即可.
解答 解:∵BD=2DC,
∴S△CGD=$\frac{1}{2}$S△BGD=$\frac{1}{2}$×8=4;
∵E是AC的中点,
∴S△CGE=S△BGE=3,
∴S△BCE=S△BGD+S△CGD+S△CGE
=8+4+3
=15,
∴△ABC的面积是:15×2=30.
故S△ABC为30.
点评 此题主要考查了三角形的面积的求法,以及三角形的中线的特征,要熟练掌握,解答此题的关键是要明确:(1)三角形的中线将三角形分成面积相等的两部分;(2)两个三角形的高相同时,面积的比等于它们的底边的比.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
1.$\sqrt{x+1}$在实数范围内有意义,则x应满足的条件是( )
| A. | x>1 | B. | x≥1 | C. | x>-1 | D. | x≥-1 |
 如图,M是?ABCD的AB边的中点,CM与BD相交于点E,连接DM,设?ABCD的面积为1,求图中阴影部分的面积.
如图,M是?ABCD的AB边的中点,CM与BD相交于点E,连接DM,设?ABCD的面积为1,求图中阴影部分的面积.