Question

16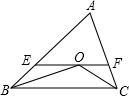．如图：已知：△ABC中，∠ABC、∠ACB的平分线，交于点O，过点O画EF∥BC交AB于点E，AC于点F；若∠ABC=60°，∠ACB=80°，求∠A、∠BOC的度数．

Answer 1

分析 由∠ABC=60°，∠ACB=80°结合三角形内角和为180°可得出∠A的度数，由角平分线的定义可知∠OBC和∠OCB的度数，根据三角形内角和为180°即可得出∠BOC的度数．

解答 解：∵∠ABC=60°，∠ACB=80°，
∴∠A=180°-∠ABC-∠ACB=40°．
∵BO平分∠ABC，CO平分∠ACB，
∴∠OBC=$\frac{1}{2}$∠ABC=30°，∠OCB=$\frac{1}{2}$∠ACB=40°，
∴∠BOC=180°-∠OBC-∠OCB=110°．

点评 本题考查了三角形内角和定理以及角平分线的定义，解题的关键是根据三角形内角和为180°算出∠A、∠BOC的度数．本题属于基础题，难度不大，解决该题型题目时，根据角与角之间的数量关系求出结论．