题目内容
14. 如图,已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
如图,已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 连接OC,先求出∠POC,再利用切线性质得到∠PCO=90°,由此可以求出∠P.
解答 解:如图,连接OC.
∵OA=OC,
∴∠OAC=∠OCA=35°,
∴∠POC=∠OAC+∠OCA=70°,
∵PC是⊙O切线,
∴PC⊥OC,
∴∠PCO=90°,
∴∠P=90°-∠POC=20°,
故选B.
点评 本题考查切线的性质、等腰三角形的性质等知识,记住切线垂直于过切点的半径,直角三角形两锐角互余,属于基础题,中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.盐城城市快速路网是我市建市史上单项投资规模最大的城市交通工程建设项目,计划2016年底建成通车,项目预算投资130亿元,130亿用科学记数法表示为( )
| A. | 130×108 | B. | 1.3×109 | C. | 1.3×1010 | D. | 1.3×1011 |
2.下列各式中与$\sqrt{12}$是同类二次根式的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{32}$ | C. | $\sqrt{18}$ | D. | $\sqrt{75}$ |
3. 如图,AB∥CD,AE交CD于C,∠A=35°,∠DEC=90°,则∠D的度数为( )
如图,AB∥CD,AE交CD于C,∠A=35°,∠DEC=90°,则∠D的度数为( )
 如图,AB∥CD,AE交CD于C,∠A=35°,∠DEC=90°,则∠D的度数为( )
如图,AB∥CD,AE交CD于C,∠A=35°,∠DEC=90°,则∠D的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
4.记n边形(n>3)的一个外角的度数为p,与该外角不相邻的(n-1)个内角的度数的和为q,则p与q的关系是( )
| A. | p=q | B. | p=q-(n-1)•180° | C. | p=q-(n-2)•180° | D. | p=q-(n-3)•180° |
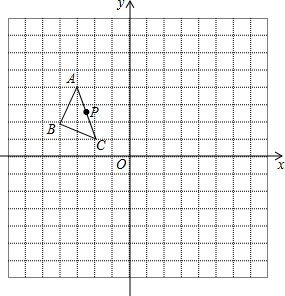 如图,△ABC三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1).
如图,△ABC三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1). 如图是由几个正方体组成的立体图形,则这个立方体从左看到的平面图形是( )
如图是由几个正方体组成的立体图形,则这个立方体从左看到的平面图形是( )


