题目内容
3．
如图，AB∥CD，AE交CD于C，∠A=35°，∠DEC=90°，则∠D的度数为（ ）| A． | 65° | B． | 55° | C． | 45° | D． | 35° |
分析 先根据平行线的性质求出∠DCE的度数，再由直角三角形的性质即可得出结论．
解答 解：∵AB∥CD，∠A=35°，
∴∠DCE=∠A=35°．
∵∠DEC=90°，
∴∠D=90°-∠DCE=90°-35°=55°．
故选B．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．
练习册系列答案
阅读快车系列答案
相关题目
14．
如图，已知⊙O的直径AB与弦AC的夹角为35°，过C点的切线PC与AB的延长线交于点P，则∠P等于（ ）
如图，已知⊙O的直径AB与弦AC的夹角为35°，过C点的切线PC与AB的延长线交于点P，则∠P等于（ ）| A． | 15° | B． | 20° | C． | 25° | D． | 30° |
11．
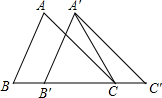如图，在△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿着射线BC的方向平移2个单位后，得到△A′B′C′，连接A′C，则△A′B′C的面积是（ ）
如图，在△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿着射线BC的方向平移2个单位后，得到△A′B′C′，连接A′C，则△A′B′C的面积是（ ）| A． | 4 | B． | 2$\sqrt{3}$ | C． | 4$\sqrt{3}$ | D． | 8$\sqrt{3}$ |
18．
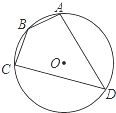如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为4，∠B=135°，则弧AC的长（ ）
如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为4，∠B=135°，则弧AC的长（ ）| A． | 2π | B． | π | C． | $\frac{π}{2}$ | D． | 4π |
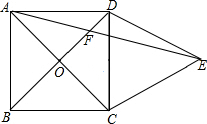如图，正方形ABCD，△DCE是等边三角形，AC、BD交于点O，AE交BD于点F．
已知：如图，在平行四边形ABCD中，O为对角线BD的中点，过点O的作直线EF⊥BD分别交AD，BC于E，F两点，连结BE，DF．求证：四边形BFDE为菱形．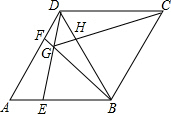
如图，在菱形ABCD中，AB=BD，点E，F分别在AB，AD上，且AE=DF，连接BF与DE相交于点G，连接CG与BD相交于点H．下列结论：
13．
如图是一个正方体的展开图，把展开图折叠成正方体后，“你”字一面相对的面上的字是（ ）
如图是一个正方体的展开图，把展开图折叠成正方体后，“你”字一面相对的面上的字是（ ）| A． | 梦 | B． | 我 | C． | 中 | D． | 国 |