题目内容
15.解下列不等式组.$\left\{\begin{array}{l}{x-\frac{x-1}{2}>2x-5}\\{x+1≥3x-2}\end{array}\right.$.分析 本题可根据不等式组分别求出x的取值,然后画出数轴,数轴上相交的点的集合就是该不等式的解集.若没有交点,则不等式无解.
解答 解:$\left\{\begin{array}{l}{x-\frac{x-1}{2}>2x-5①}\\{x+1≥3x-2②}\end{array}\right.$
由①得,x$<\frac{11}{3}$,
由②得,x$≤\frac{3}{2}$,
所以,不等式组的解集是x$≤\frac{3}{2}$.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x大于较小的数、小于较大的数,那么解集为x介于两数之间.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
6.下列图形中,是中心对称图形,但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.下列图形中,一定是轴对称图形的是( )
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 直角三角形 |
10.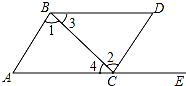 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠D+∠ACD=180° | C. | ∠D=∠DCE | D. | ∠1=∠2 |
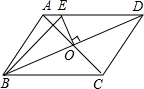 如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OE⊥BD,交AD于点E,如果△ABE的周长为4,那么平行四边形ABCD的周长是8.
如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OE⊥BD,交AD于点E,如果△ABE的周长为4,那么平行四边形ABCD的周长是8. 如图,在平面直角坐标系,正方形OABC的顶点O在坐标原点,顶点C、A分别在x轴、y轴的正半轴上,边长为4,点N是边BC的中点,点D是OC的中点.
如图,在平面直角坐标系,正方形OABC的顶点O在坐标原点,顶点C、A分别在x轴、y轴的正半轴上,边长为4,点N是边BC的中点,点D是OC的中点.