题目内容
9. 已知:如图,△ABC中,AC=8,点D在AB边上,且AD=BD=CD=5,在△ABC外,作等边△ACE.
已知:如图,△ABC中,AC=8,点D在AB边上,且AD=BD=CD=5,在△ABC外,作等边△ACE.(1)判断△ABC的形状,并证明;
(2)求四边形ABCE的周长.
分析 (1)由等腰三角形的性质和三角形内角和定理即可得出结论;
(2)由勾股定理求出BC,再由等边三角形的性质即可得出结果.
解答 解:(1)结论:△ABC的是直角三角形;
∵AD=BD=CD,
∴∠1=∠2,∠3=∠4,…(2分)
∴∠1+∠4=∠2+∠3,
又∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∴△ABC是直角三角形.
(2)在直角三角形△ABC中,AC=8,AB=10,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=6,
又∵△ACE是等边三角形.
∴AE=CE=8,
∴四边形ABCE的周长为AB+BC+AE+CE=32.
点评 本题考查了等边三角形的性质、等腰三角形的性质、三角形内角和定理、勾股定理;熟练掌握等边三角形的性质和等腰三角形的性质是解决问题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
19. 如图是一个正方体的表面展开图,相对面上两个数互为相反数,则x+y=( )
如图是一个正方体的表面展开图,相对面上两个数互为相反数,则x+y=( )
 如图是一个正方体的表面展开图,相对面上两个数互为相反数,则x+y=( )
如图是一个正方体的表面展开图,相对面上两个数互为相反数,则x+y=( )| A. | 6 | B. | -5 | C. | 7 | D. | -6 |
20. 2016年6月20日,新一期全球超级计算机500强榜单公布,使用中国自主芯片制造的“神威太湖之光”取代“天河二号”登上榜首,中国超算上榜总数量也有史以来首次超过美国名列第一.据国际TOP500组织当天发布的榜单,“神威太湖之光”的浮点运算速度为每秒930000000亿次,不仅速度比第二名“天河二号”快出近两倍,其效率也提高3倍.930000000亿次用科学记数法可表示为( )亿次.
2016年6月20日,新一期全球超级计算机500强榜单公布,使用中国自主芯片制造的“神威太湖之光”取代“天河二号”登上榜首,中国超算上榜总数量也有史以来首次超过美国名列第一.据国际TOP500组织当天发布的榜单,“神威太湖之光”的浮点运算速度为每秒930000000亿次,不仅速度比第二名“天河二号”快出近两倍,其效率也提高3倍.930000000亿次用科学记数法可表示为( )亿次.
 2016年6月20日,新一期全球超级计算机500强榜单公布,使用中国自主芯片制造的“神威太湖之光”取代“天河二号”登上榜首,中国超算上榜总数量也有史以来首次超过美国名列第一.据国际TOP500组织当天发布的榜单,“神威太湖之光”的浮点运算速度为每秒930000000亿次,不仅速度比第二名“天河二号”快出近两倍,其效率也提高3倍.930000000亿次用科学记数法可表示为( )亿次.
2016年6月20日,新一期全球超级计算机500强榜单公布,使用中国自主芯片制造的“神威太湖之光”取代“天河二号”登上榜首,中国超算上榜总数量也有史以来首次超过美国名列第一.据国际TOP500组织当天发布的榜单,“神威太湖之光”的浮点运算速度为每秒930000000亿次,不仅速度比第二名“天河二号”快出近两倍,其效率也提高3倍.930000000亿次用科学记数法可表示为( )亿次.| A. | 9.3×108 | B. | 9.3×107 | C. | 93×107 | D. | 0.93×109 |
17.当x满足( )时,$\frac{\sqrt{1+x}}{x}$在实数范围内有意义.
| A. | x>-1 | B. | x≥1且x≠0 | C. | x≥-1 | D. | x≥-1且x≠0 |
19.能说明命题“对于任何实数a,a2≥a”是假命题的一个反例可以是( )
| A. | a=-2 | B. | a=1 | C. | a=0 | D. | a=0.2 |
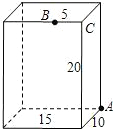 如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )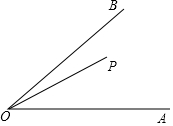 如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$.
如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$.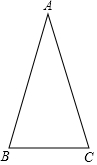 已知:如图,△ABC是等腰三角形,AB=AC,现要在AB边上确定一点D,使点D到点A的距离与点D到点C的距离相等.
已知:如图,△ABC是等腰三角形,AB=AC,现要在AB边上确定一点D,使点D到点A的距离与点D到点C的距离相等. 如图AB+AC>BC一定成立,其依据是两点之间,线段最短.若∠1+∠2=180°,∠3+∠2=180°,∠1=55°,则∠3=55°,其依据是同角的补角相等.90°-21°13′24″=68°46′36″.
如图AB+AC>BC一定成立,其依据是两点之间,线段最短.若∠1+∠2=180°,∠3+∠2=180°,∠1=55°,则∠3=55°,其依据是同角的补角相等.90°-21°13′24″=68°46′36″.