题目内容
17.对于任意不相等的两个数a,b,定义一种运算◎如下:a◎b=$\frac{b-a}{{\sqrt{a}+b}}$,则3◎2=$\sqrt{3}$-2.分析 首先根据新运算◎:a◎b=$\frac{b-a}{{\sqrt{a}+b}}$,可得3◎2=$\frac{2-3}{\sqrt{3}+2}$;然后根据分母有理化的方法,求出3◎2的值是多少即可.
解答 解:3◎2
=$\frac{2-3}{\sqrt{3}+2}$
=-$\frac{1}{\sqrt{3}+2}$
=-$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$
=-(2-$\sqrt{3}$)
=$\sqrt{3}-2$
故答案为:$\sqrt{3}$-2.
点评 (1)此题主要考查了分母有理化的含义,以及分母有理化的方法,要熟练掌握.
(2)此题还考查了对新运算a◎b=$\frac{b-a}{{\sqrt{a}+b}}$的掌握和应用,要掌握它的运算方法.

练习册系列答案
相关题目
2.下列计算,正确的是( )
| A. | $\sqrt{8}-\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{4}+\sqrt{9}=\sqrt{13}$ | C. | $3\sqrt{2}-\sqrt{2}=2\sqrt{2}$ | D. | $2+\sqrt{2}=2\sqrt{2}$ |
7.下列等式从左到右的变形,属于因式分解的是( )
| A. | x3-x=x(x+1)(x-1) | B. | x2+2x+1=x(x+2)+1 | C. | (x+1)(x+3)=x2+4x+3 | D. | a(x-y)=ax-ay |
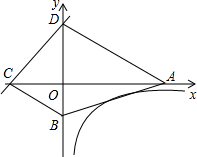 如图所示,已知点A(4,0),点B在y轴上,经过A、B两点的直线与反比例函数y=$\frac{k}{x}$(k≤-1)在第四象限的图象只有一个公共点.又一次函数y=x-2k的图象与x轴、y轴分别交于点C、D两点.当四边形ABCD的面积最小时,求k的值及面积的最小值.
如图所示,已知点A(4,0),点B在y轴上,经过A、B两点的直线与反比例函数y=$\frac{k}{x}$(k≤-1)在第四象限的图象只有一个公共点.又一次函数y=x-2k的图象与x轴、y轴分别交于点C、D两点.当四边形ABCD的面积最小时,求k的值及面积的最小值.