题目内容
8.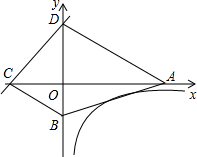 如图所示,已知点A(4,0),点B在y轴上,经过A、B两点的直线与反比例函数y=$\frac{k}{x}$(k≤-1)在第四象限的图象只有一个公共点.又一次函数y=x-2k的图象与x轴、y轴分别交于点C、D两点.当四边形ABCD的面积最小时,求k的值及面积的最小值.
如图所示,已知点A(4,0),点B在y轴上,经过A、B两点的直线与反比例函数y=$\frac{k}{x}$(k≤-1)在第四象限的图象只有一个公共点.又一次函数y=x-2k的图象与x轴、y轴分别交于点C、D两点.当四边形ABCD的面积最小时,求k的值及面积的最小值.
分析 首先设经过点A(4,0)的直线的函数表达式为y=m(x-4)(m≠0),由直线与反比例函数图象只有一个公共点,可联立$\left\{\begin{array}{l}{y=\frac{k}{x}}\\{y=m(x-4)}\end{array}\right.$,整理得mx2-4mx-k=0,然后由判别式△=(-4m)2-4m•(-k)=16m2+4mk=0,求得m=-$\frac{1}{4}$k,继而求得点B,C,D的坐标,即可求得AC与BD的长,继而可得S四边形ABCD=$\frac{1}{2}$BD•AC=$\frac{1}{2}$(-3k)(4-2k),然后由二次函数的最值,求得答案.
解答 解:设经过点A(4,0)的直线的函数表达式为y=m(x-4)(m≠0),
由$\left\{\begin{array}{l}{y=\frac{k}{x}}\\{y=m(x-4)}\end{array}\right.$,可得:mx2-4mx-k=0,
∵直线与反比例函数图象只有一个公共点,
∴△=(-4m)2-4m•(-k)=16m2+4mk=0,
解得:m=-$\frac{1}{4}$k,
∴经过点A(4,0)的直线的函数表达式为:y=-$\frac{1}{4}$k(x-4),
∴点B的坐标为:(0,k),
∵一次函数y=x-2k的图象与x轴、y轴分别交于点C、D两点,
∴点C(2k,0),点D(0,-2k),
∴AC=4-2k,BD=-2k-k=-3k,
∴S四边形ABCD=$\frac{1}{2}$BD•AC=$\frac{1}{2}$(-3k)(4-2k)=3k2-6k=3(k-1)2-3,
∵k≤-1,
∴当k=-1时,S四边形ABCD有最小值,最小值等于9.
点评 此题属于反比例函数综合题,考查了反比例函数与一次函数的交点问题、根的判别式以及二次函数的最值问题.注意设经过点A(4,0)的直线的函数表达式为y=m(x-4)(m≠0),利用直线与反比例函数图象只有一个公共点,求得k与m的关系,表示出B,C,D的坐标是关键.

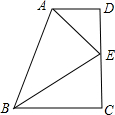 如图,在四边形ABCD中,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则下列结论中错误的是( )
如图,在四边形ABCD中,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则下列结论中错误的是( )| A. | AE⊥BE | B. | CE=DE | C. | AD+DE=BE | D. | AB=AD+BC |
(1)请根据题意填写下表(填写表中所有空格):
| 运往甲地 | 运往乙地 | |
| A | ||
| B |
(3)按照题(2)的调运方案,从A基地往甲中心运送粮食,在运输途中的E地接到F地商家的一个电话,该商家需要25吨.已知A基地与E地之间的运费为每吨520元,甲中心与F地之间的运费为每吨480元.现A基地有两种方案运送到甲中心和F地商家:
方案一:从E地直接运送到F地商家,运到后把剩下的粮食运到甲中心;
方案二:先把粮食运到甲中心,再运25吨到F地商家.
若方案一比方案二的总运费多21000元,则从E地到F地商家的运费是每吨多少元?
