题目内容
在半径为2的圆中,弦AC长为1,M为AC中点,过M点最长的弦为BD,则四边形ABCD的面积为 .
考点:垂径定理,勾股定理
专题:计算题
分析:先由直径是圆中最长的弦得出BD=4,再根据垂径定理的推论得出AC⊥BD,则四边形ABCD的面积=
AC•BD.
| 1 |
| 2 |
解答: 解:如图.∵M为AC中点,过M点最长的弦为BD,
解:如图.∵M为AC中点,过M点最长的弦为BD,
∴BD是直径,BD=4,且AC⊥BD,
∴四边形ABCD的面积=
AC•BD=
×1×4=2.
故答案为:2.
 解:如图.∵M为AC中点,过M点最长的弦为BD,
解:如图.∵M为AC中点,过M点最长的弦为BD,∴BD是直径,BD=4,且AC⊥BD,
∴四边形ABCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:2.
点评:本题考查了垂径定理,四边形的面积,难度适中.得出BD是直径是解题的关键.

练习册系列答案
相关题目
 如图,已知∠l+∠2=150°,则∠α+∠β=( )
如图,已知∠l+∠2=150°,则∠α+∠β=( )| A、等于150° |
| B、等于210° |
| C、等于250° |
| D、值不能确定 |
 如图,用火柴棍连续搭建三角形和正方形,公共边只用一根火柴棍.如果搭建三角形和正方形共用了77根火柴棍,并且三角形的个数比正方形的个数少5个,那么一共能连续搭建三角形、正方形各多少个?
如图,用火柴棍连续搭建三角形和正方形,公共边只用一根火柴棍.如果搭建三角形和正方形共用了77根火柴棍,并且三角形的个数比正方形的个数少5个,那么一共能连续搭建三角形、正方形各多少个? 如图,在Rt△ABC中,∠C=90°,AB=6,BC=4,则cosB=
如图,在Rt△ABC中,∠C=90°,AB=6,BC=4,则cosB=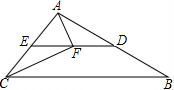 如图,在△ABC中,∠ACB=58°,D,E分别是AB,AC中点.点F在线段DE上,且AF⊥CF,则∠FAE=
如图,在△ABC中,∠ACB=58°,D,E分别是AB,AC中点.点F在线段DE上,且AF⊥CF,则∠FAE= 服装厂为了估计某校七年级学生穿每种尺码校服的人数,从该校七年级学生中随机抽取了50名学生的身高数据(单位:cm),绘制成了下面的频数分布表和频数分布直方图.
服装厂为了估计某校七年级学生穿每种尺码校服的人数,从该校七年级学生中随机抽取了50名学生的身高数据(单位:cm),绘制成了下面的频数分布表和频数分布直方图.