题目内容
19.下列计算结果正确的是( )| A. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | B. | $\sqrt{{a}^{2}-{b}^{2}}$=a-b | C. | $\sqrt{8}$-$\sqrt{18}$=-$\sqrt{2}$ | D. | $\frac{\sqrt{6}+\sqrt{8}}{2}$=$\sqrt{3}$+2 |
分析 根据二次根式的加减,可得答案.
解答 解:A、被开方数不能相加减,故A错误;
B、$\sqrt{(a-b)^{2}}$=|a-b|,故B错误;
C、$\sqrt{8}$-$\sqrt{18}$=2$\sqrt{2}$-3$\sqrt{2}$=-$\sqrt{2}$,故C正确;
D、分子分母除以不同的数,故D错误;
故选:C.
点评 本题考查了二次根式的加减,熟记法则并根据法则计算是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知,a、b、c是三角形的边长,如果(a-6)2+$\sqrt{b-8}$+|c-10|=0,下列说法中不正确的是( )
| A. | 这个三角形是直角三角形 | B. | 这个三角形最长边为10 | ||
| C. | 这个三角形的面积为48 | D. | 这个三角形的最长边上的高为4.8 |
10.点M(1,-2)关于原点对称的点的坐标是( )
| A. | (-1,2) | B. | (1,2) | C. | (-1,-2) | D. | (-2,1) |
14.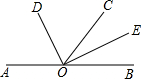 如图,O是直线AB上的一点,过点O作射线OC,OD平分∠AOC,OE平分∠BOC,若∠DOC=50°,则∠BOE的度数为( )
如图,O是直线AB上的一点,过点O作射线OC,OD平分∠AOC,OE平分∠BOC,若∠DOC=50°,则∠BOE的度数为( )
 如图,O是直线AB上的一点,过点O作射线OC,OD平分∠AOC,OE平分∠BOC,若∠DOC=50°,则∠BOE的度数为( )
如图,O是直线AB上的一点,过点O作射线OC,OD平分∠AOC,OE平分∠BOC,若∠DOC=50°,则∠BOE的度数为( )| A. | 50° | B. | 40° | C. | 25° | D. | 20° |
4.若3x-2y=0,则$\frac{x}{y}$-1等于( )
| A. | $-\frac{1}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{3}$ | D. | $\frac{2}{3}$ |
11.若分式$\frac{1}{x(x+1)}$有意义,则x满足的条件是( )
| A. | x≠0 | B. | x≠1 | C. | x≠-1 | D. | x≠0,x≠-1 |
8. 如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,$\sqrt{3}$),则点C的坐标是( )
如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,$\sqrt{3}$),则点C的坐标是( )
 如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,$\sqrt{3}$),则点C的坐标是( )
如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,$\sqrt{3}$),则点C的坐标是( )| A. | (0,2) | B. | (0,5) | C. | (0,$\sqrt{5}$) | D. | (0,$\sqrt{3}$+$\sqrt{2}$) |
9.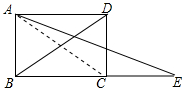 如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E的度数是( )
如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E的度数是( )
 如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E的度数是( )
如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E的度数是( )| A. | 45° | B. | 30° | C. | 20° | D. | 15° |
 如图,数轴上有A、B、C、D四个整数点(即各点均表示整数),且3AB=BC=2CD.若A、D两点所表示的数分别是-6和5,则线段AC的中点所表示的数是( )
如图,数轴上有A、B、C、D四个整数点(即各点均表示整数),且3AB=BC=2CD.若A、D两点所表示的数分别是-6和5,则线段AC的中点所表示的数是( )