题目内容
9.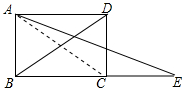 如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E的度数是( )
如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E的度数是( )| A. | 45° | B. | 30° | C. | 20° | D. | 15° |
分析 连接AC,由矩形性质可得∠E=∠DAE、BD=AC=CE,知∠E=∠CAE,而∠ADB=∠CAD=30°,可得∠E度数
解答 解:连接AC,如图所示:
∵四边形ABCD是矩形,
∴AD∥BE,AC=BD,且∠ADB=∠CAD=30°,
∴∠E=∠DAE,
又∵BD=CE,
∴CE=CA,
∴∠E=∠CAE,
∵∠CAD=∠CAE+∠DAE,
∴∠E+∠E=30°,
∴∠E=15°,
故选:D.
点评 本题主要考查矩形性质、等腰三角形的性质,熟练掌握矩形对角线相等且互相平分、对边平行是解题关键.

练习册系列答案
相关题目
19.下列计算结果正确的是( )
| A. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | B. | $\sqrt{{a}^{2}-{b}^{2}}$=a-b | C. | $\sqrt{8}$-$\sqrt{18}$=-$\sqrt{2}$ | D. | $\frac{\sqrt{6}+\sqrt{8}}{2}$=$\sqrt{3}$+2 |
20.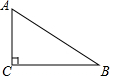 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )
 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 相切或相交 |
17. 如图,在△ABC中,点D,E分别在AC,AB上且DE∥BC,若S△ADE:S△BDE=2:3,则S△ADE:S△ACB=( )
如图,在△ABC中,点D,E分别在AC,AB上且DE∥BC,若S△ADE:S△BDE=2:3,则S△ADE:S△ACB=( )
 如图,在△ABC中,点D,E分别在AC,AB上且DE∥BC,若S△ADE:S△BDE=2:3,则S△ADE:S△ACB=( )
如图,在△ABC中,点D,E分别在AC,AB上且DE∥BC,若S△ADE:S△BDE=2:3,则S△ADE:S△ACB=( )| A. | 2:3 | B. | 4:9 | C. | 4:25 | D. | 4:19 |
4.方程x2-x=0的解是( )
| A. | x=0 | B. | x=1 | C. | x1=0,x2=1 | D. | x1=0,x2=-1 |
14.甲地到乙地之间的铁路长210千米,动车运行后的平均速度是原来火车的1.6倍,这样由甲地到乙地的行驶时间缩短了1.5小时,设原来火车的平均速度为x千米/小时,则下列方程正确的是( )
| A. | $\frac{210}{x}$-1.5=$\frac{210}{1.6x}$ | B. | $\frac{210}{x}$+1.6=$\frac{210}{1.5x}$ | ||
| C. | $\frac{210}{x}$+1.5=$\frac{210}{1.6x}$ | D. | $\frac{210}{x}$-1.6=$\frac{210}{1.5x}$ |
1.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为220元,按标价的五折销售,仍可获利10%,则这件商品的进价为( )
| A. | 120元 | B. | 100元 | C. | 80元 | D. | 60元 |
18.解方程$\frac{3x+2}{4}$-$\frac{5x+1}{12}$=1-$\frac{2x-1}{2}$时,去分母正确的是( )
| A. | 3(3x+2)-5x+1=12-6(2x-1) | B. | 3(3x+2)-5x-1=1-6(2x-1) | ||
| C. | 3(3x+2)-5x-1=12-6(2x-1) | D. | (3x+2)-5x+1=12-6(2x-1) |