题目内容
9.一元二次方程ax2+3x-1=0有两个不等实根,则a的取值范围是( )| A. | a<-$\frac{9}{4}$ | B. | a≥-$\frac{9}{4}$且a≠0 | C. | a>-$\frac{9}{4}$且a≠0 | D. | a>-$\frac{9}{4}$ |
分析 根据一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac意义,由题意得△>0,可得关于a的不等式32+4a>0,且二次项系数不能为0,解不等式可得答案.
解答 解:∵一元二次方程ax2+3x-1=0有两个不等实根,
∴32+4a>0,且a≠0,
解得a>-$\frac{9}{4}$且a≠0,
故选C.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
1.已知抛物线y=-x2+6x-5,它的顶点坐标为( )
| A. | (-3,4) | B. | (3,-4) | C. | (-3,-4) | D. | (3,4) |
18.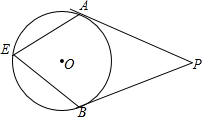 如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=50°,则∠P为( )
如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=50°,则∠P为( )
 如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=50°,则∠P为( )
如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=50°,则∠P为( )| A. | 130° | B. | 80° | C. | 50° | D. | 45° |
 )2014×1.52013×(﹣1)2015的结果是( )
)2014×1.52013×(﹣1)2015的结果是( ) B.
B.  C. ﹣
C. ﹣ D. ﹣
D. ﹣
 如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M,当 OM=4cm时,⊙M与OA相切.
如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M,当 OM=4cm时,⊙M与OA相切.