题目内容
3. 如图,在△ABC中,点D是BC边上的点,且CD=2BD,如果$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(用含$\overrightarrow a$、$\overrightarrow b$的式子表示).
如图,在△ABC中,点D是BC边上的点,且CD=2BD,如果$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(用含$\overrightarrow a$、$\overrightarrow b$的式子表示).
分析 由$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,直接利用三角形法则即可求得$\overrightarrow{BD}$,再由CD=2BD,即可求得答案.
解答 解:∵$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,
∴$\overrightarrow{BD}$=$\overrightarrow{AD}$-$\overrightarrow{AB}$=$\overrightarrow{b}$-$\overrightarrow{a}$,
∵在△ABC中,点D是BC边上的点,且CD=2BD,
∴$\overrightarrow{BC}$=3$\overrightarrow{BD}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$.
故答案为:$3\overrightarrow b-3\overrightarrow a$.
点评 此题考查了平面向量的知识.注意掌握三角形法则的应用是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图,?ABCD中,∠C=110°,BE平分∠ABC,则∠AEB等于( )
如图,?ABCD中,∠C=110°,BE平分∠ABC,则∠AEB等于( )
 如图,?ABCD中,∠C=110°,BE平分∠ABC,则∠AEB等于( )
如图,?ABCD中,∠C=110°,BE平分∠ABC,则∠AEB等于( )| A. | 11° | B. | 35° | C. | 55° | D. | 70° |

 如图,D、E在△ABC的边上,如果ED∥BC,AE:BE=1:2,BC=6,那么$\overrightarrow{DE}$的模为( )
如图,D、E在△ABC的边上,如果ED∥BC,AE:BE=1:2,BC=6,那么$\overrightarrow{DE}$的模为( )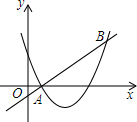 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),不等式x2+bx+c<x+m的解集为1<x<3.
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),不等式x2+bx+c<x+m的解集为1<x<3.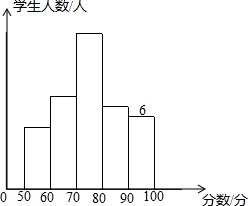 某校同学参加语文知识竞赛,将学生的成绩,进行整理后分成5组,绘制成频数分布直方图如下,图中从左到右各小组的频率分别是0.0625,0.25,0.375,0.1875,0.125且已知最右边小组的频数为6,结合直方图提供的信息,解答下列问题:
某校同学参加语文知识竞赛,将学生的成绩,进行整理后分成5组,绘制成频数分布直方图如下,图中从左到右各小组的频率分别是0.0625,0.25,0.375,0.1875,0.125且已知最右边小组的频数为6,结合直方图提供的信息,解答下列问题: