Question

18．在△ABC中，最大∠A是最小∠C的2倍，且AB=2，AC=3，则BC的长为$\sqrt{10}$．

Answer 1

分析 作出∠A的平分线AD，利用相似三角形的判定得出△BAD∽△BCA，进而得出$\frac{BA}{BC}=\frac{AD}{AC}=\frac{BD}{AB}$，从而得出6=AD•BC，2AD=3（BC-AD），进而得出BC的值．

解答 解：如图，作∠A的平分线AD，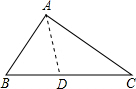

∵最大角∠A是最小角∠C的两倍，
∴∠BAD=∠DAC=∠C，
∴AD=CD，
∵∠BAC=2∠C，
∴∠BAD=∠C，
又∵∠B=∠B，
∴△BAD∽△BCA，
∴$\frac{BA}{BC}=\frac{AD}{AC}=\frac{BD}{AB}$，
∴$\frac{2}{BC}=\frac{AD}{3}=\frac{BC-AD}{2}$，
∴6=AD•BC，2AD=3（BC-AD），
解得：AD=$\frac{6}{BC}$，
∴CB=$\sqrt{10}$．

点评 此题主要考查了相似三角形的判定与性质，作出辅助线后利用相似三角形性质求出是解决问题的关键．