题目内容
8．
如图，D、E在△ABC的边上，如果ED∥BC，AE：BE=1：2，BC=6，那么$\overrightarrow{DE}$的模为（ ）| A． | -2 | B． | -3 | C． | 2 | D． | 3 |
分析 由ED∥BC，可证得△AED∽△ABC，然后根据相似三角形的对应边成比例，求得ED：BC=1：3，则可得$\overrightarrow{DE}$=-$\frac{1}{3}$$\overrightarrow{BC}$，又由BC=6，即可求得$\overrightarrow{DE}$的模．
解答 解：∵ED∥BC，
∴△AED∽△ABC，
∴ED：BC=AE：AB，
∵AE：BE=1：2，
∴AE：AB=1：3，
∴ED：BC=1：3，
∴$\overrightarrow{DE}$=-$\frac{1}{3}$$\overrightarrow{BC}$，
∵BC=6，
∴|$\overrightarrow{DE}$|=$\frac{1}{3}$|$\overrightarrow{BC}$|=2．
故选C．
点评 此题考查了平面向量的知识以及相似三角形的判定与性质．注意利用相似三角形的性质，求得$\overrightarrow{DE}$=$\frac{1}{3}$$\overrightarrow{BC}$是解此题的关键．
练习册系列答案
相关题目
16．
如图，在平行四边形ABCD中，对角线AC与BD相交于点O，如果$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$．那么下列选项中，正确的是（ ）
如图，在平行四边形ABCD中，对角线AC与BD相交于点O，如果$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$．那么下列选项中，正确的是（ ）| A． | $\overrightarrow{OC}$=$\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{b}$） | B． | $\overrightarrow{OA}$=$\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{b}$） | C． | $\overrightarrow{OD}$=$\frac{1}{2}$（$\overrightarrow{a}$-$\overrightarrow{b}$） | D． | $\overrightarrow{BD}$=（$\overrightarrow{a}$-$\overrightarrow{b}$） |
如图，在△ABC中，点D是BC边上的点，且CD=2BD，如果$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AD}=\overrightarrow b$，那么$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$（用含$\overrightarrow a$、$\overrightarrow b$的式子表示）．
13．若四边形ABCD的对角线交于点O，且有$\overrightarrow{AB}=2\overrightarrow{DC}$，则以下结论正确的是（ ）
| A． | $\overrightarrow{AO}=2\overrightarrow{OC}$ | B． | $|\overrightarrow{AC}|=|\overrightarrow{BD}|$ | C． | $\overrightarrow{AC}=\overrightarrow{BD}$ | D． | $\overrightarrow{DO}=2\overrightarrow{OB}$ |
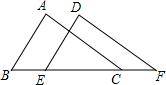如图，在△ABC和△DEF，若AB=DE，BE=CF，要使△ABC≌△DEF，还需添加一个条件（只要写出一个就可以）是∠B=∠DEF．