题目内容
12．
如图，?ABCD中，∠C=110°，BE平分∠ABC，则∠AEB等于（ ）| A． | 11° | B． | 35° | C． | 55° | D． | 70° |
分析 由平行四边形ABCD中，∠C=110°，可求得∠ABC的度数，又由BE平分∠ABC，即可求得∠CBE的度数，然后由平行线的性质，求得答案．
解答 解：∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥BC，
∵∠C=110°，
∴∠ABC=180°-∠C=70°，
∵BE平分∠ABC，
∴∠CBE=$\frac{1}{2}$∠ABC=35°，
∴∠AEB=∠CBE=35°．
故选B．
点评 此题考查了平行四边形的性质，属于基础题，解答本题的关键是掌握平行四边形邻角互补的性质，难度一般．
练习册系列答案
小学课时特训系列答案
相关题目
如图，在△ABC中，点D是BC边上的点，且CD=2BD，如果$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AD}=\overrightarrow b$，那么$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$（用含$\overrightarrow a$、$\overrightarrow b$的式子表示）．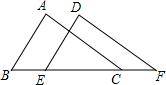
如图，在△ABC和△DEF，若AB=DE，BE=CF，要使△ABC≌△DEF，还需添加一个条件（只要写出一个就可以）是∠B=∠DEF．
7．
实数a、b、c在数轴上的位置如图所示，则下列式子中一定成立的是（ ）
实数a、b、c在数轴上的位置如图所示，则下列式子中一定成立的是（ ）| A． | a+b+c＞0 | B． | |a+b|＜c | C． | |a-c|=|a|+c | D． | |b-c|＞|c-a| |
如图，AD⊥BC，垂足为D，BE⊥AC，垂足为E，AD与BE相交于点F，连接ED．
2．下列各图中，能正确表示数轴的是（ ）
| A． |  | B． |  | C． |  | D． |  |