题目内容
18．分解因式：2x2-4x-1=2（x-$\frac{2+\sqrt{6}}{2}$）（x-$\frac{2-\sqrt{6}}{2}$）．分析 令多项式等于0，求出x的值，即可确定出分解因式的结果．
解答 解：令2x2-4x-1=0，
解得：x=$\frac{4±2\sqrt{6}}{4}$=$\frac{2±\sqrt{6}}{2}$，
则2x2-4x-1=2（x-$\frac{2+\sqrt{6}}{2}$）（x-$\frac{2-\sqrt{6}}{2}$）．
故答案为：2（x-$\frac{2+\sqrt{6}}{2}$）（x-$\frac{2-\sqrt{6}}{2}$）．
点评 此题考查了实数范围内分解因式-求根公式法，求根公式法当首项系数不是1时，往往需要多次试验，务必注意各项系数的符号．注意当无法用十字相乘法的方法时用求根公式法可分解因式．
练习册系列答案
相关题目
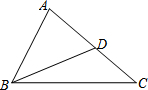如图，△ABC中，D是边AC上一点，连接BD．要使△ABD∽△ACB，需要补充的一个条件为∠ABD=∠C或∠ADB=∠ABC或AB2=AD•AC．
如图所示，△ACB≌△DEF，其中A与D，C与E是对应顶点，请写出它们的对应边和对应角．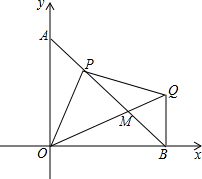
已知：如图，A、B两点坐标为（0，4），B（4，0），P为线段AB上的任一点，过P作OP的垂线与过B点的x轴的垂线交于点Q，OQ与直线AB交于点M．请探究解答下列问题：