题目内容
【题目】定义:有三条边相等的四边形称为三等边四边形.
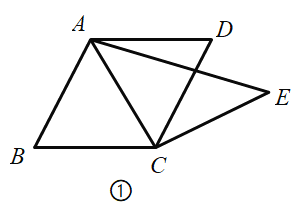
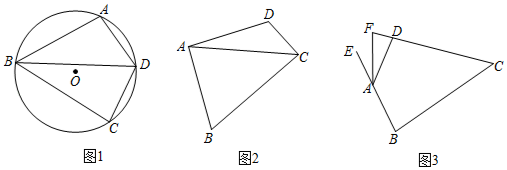
(1)如图①,平行四边形![]() 中,对角线
中,对角线![]() 平分
平分![]() ,将线段
,将线段![]() 绕点
绕点![]() 旋转一个角度
旋转一个角度![]() 至
至![]() ,连接
,连接![]() .
.
①求证:四边形![]() 是三等边四边形;
是三等边四边形;
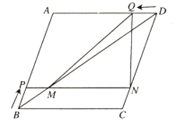
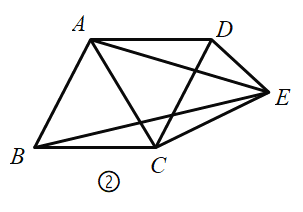
②如图②,连接![]() ,
,![]() .求证:
.求证:![]() ;
;
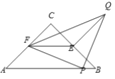
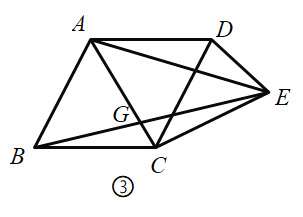
(2)如图,在(1)的条件下,设![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,求以
,求以![]() ,
,![]() 和
和![]() 为边的三角形的面积.
为边的三角形的面积.
【答案】(1)①见解析;②见解析;(2)![]()
【解析】
(1)①先证明四边形![]() 是菱形,得到
是菱形,得到![]() ,根据旋转性质得到
,根据旋转性质得到![]() ,问题得证;
,问题得证;
②如图②,延长![]() 至点
至点![]() ,得到
,得到![]() ,
,![]() 得到
得到![]() ,根据菱形性质得到
,根据菱形性质得到![]() ,问题得证;
,问题得证;
(2)如图③,连接![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,先求出
,先求出![]() 长度,判断以
长度,判断以![]() 为边的三角形为直角三角形,计算面积即可.
为边的三角形为直角三角形,计算面积即可.
解:(1)①证明:如图①,∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() ,
,
∵![]() 半分
半分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴平行四边形![]() 是菱形,
是菱形,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是三等边四边形.
是三等边四边形.

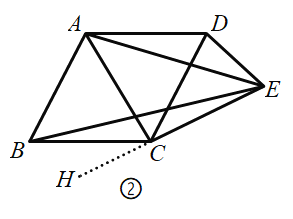
②证明:如图②,延长![]() 至点
至点![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∴![]() .
.
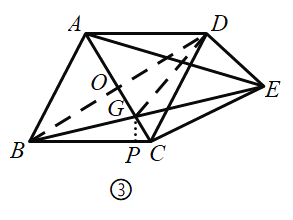
(2)如图③,连接![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
∵四边形![]() 是菱形,∴
是菱形,∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() .
.
∵![]() 垂直平分
垂直平分![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴以![]() 为边的三角形为
为边的三角形为![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
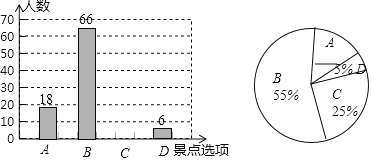
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间线上随机调查了部分学生,调查结果整理如下:
阅读时间人数统计表
阅读时间t(小时) | 人数 | 占人数百分比 |
0≤t<0.5 | 4 | 20% |
0.5≤t<1 | m | 15% |
1≤t<1.5 | 5 | 25% |
1.5≤t<2 | 6 | n |
2≤t<2.5 | 2 | 10% |
根据图表解答下列问题:
(1)此次抽样调查中,共抽取了 名学生;
(2)在阅读时间人数统计表中m= ,n= ;
(3)根据抽样调查的结果,请估计该校2000名学生中有多少名学生每天阅读时间在2≤t<2.5时间段?