题目内容
18.若代数式$\frac{5x+4}{6}$的值不小于$\frac{7}{8}$-$\frac{1-x}{3}$的值,求满足条件的x的最小整数值.分析 根据题意得出关于x的不等式,根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得x的范围,继而可得答案.
解答 解:根据题意得$\frac{5x+4}{6}$≥$\frac{7}{8}$-$\frac{1-x}{3}$,
∴4(5x+4)≥21-8(1-x),
20x+16≥21-8+8x,
20x-8x≥21-8-16,
12x≥-3,
∴x≥-$\frac{1}{4}$,
则满足条件得x的最小整数值为0.
点评 本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列因式分解正确的是( )
| A. | a2b-2a3=a(ab-2a2) | B. | x2-x+$\frac{1}{4}$=${(x-\frac{1}{2})}^{2}$ | C. | x2+2x+1=x(x+2)+1 | D. | 4x2-y2=(4x+y)(4x-y) |
7.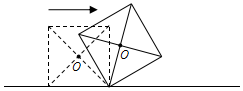 如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )
如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )
 如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )
如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )| A. | 4a | B. | 2$\sqrt{2}$πa | C. | $\sqrt{2}$πa | D. | $\sqrt{2}$a |
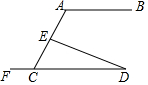 如图,AB∥CD,DE交AC于点E,下列结论:①∠A=∠ACF;②∠A=∠CED;③∠A+∠AED=180°;④∠AED>∠DCE;其中正确的个数是( )
如图,AB∥CD,DE交AC于点E,下列结论:①∠A=∠ACF;②∠A=∠CED;③∠A+∠AED=180°;④∠AED>∠DCE;其中正确的个数是( )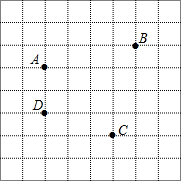 如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.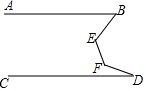 如图,AB∥CD,∠B=42°,∠D=17°,求∠E+∠F的度数.
如图,AB∥CD,∠B=42°,∠D=17°,求∠E+∠F的度数.