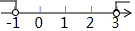题目内容
9.(1)解方程组$\left\{\begin{array}{l}{y=2x-4①}\\{3x+y=1②}\end{array}\right.$.(2)解不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3(x-1)<8-x}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)方程组利用代入消元法求出解即可.
(2)求出每个不等式的解集,根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)$\left\{\begin{array}{l}{y=2x-4①}\\{3x+y=1②}\end{array}\right.$,
①代入②得:3x+2x-4=1,
解得:x=1,
把x=1代入①得:y=-2,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1①}\\{1-3(x-1)<8-x②}\end{array}\right.$,
∵解不等式①得:x≤1,
解不等式②得:x>-2,
∴不等式组的解集为:-2<x≤1.
在数轴上表示不等式组的解集为: .
.
点评 本题考查了解一元一次不等式(组),在数轴上表示不等式组的解集的应用,关键是能根据不等式的解集找出不等式组的解集.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
14. 把一块直角三角板的直角顶点放在直尺的一边上,如图所示,现用量角器量得∠2=112°,则∠1的度数为( )
把一块直角三角板的直角顶点放在直尺的一边上,如图所示,现用量角器量得∠2=112°,则∠1的度数为( )
 把一块直角三角板的直角顶点放在直尺的一边上,如图所示,现用量角器量得∠2=112°,则∠1的度数为( )
把一块直角三角板的直角顶点放在直尺的一边上,如图所示,现用量角器量得∠2=112°,则∠1的度数为( )| A. | 30° | B. | 28° | C. | 22° | D. | 20° |
1.为了解学生的身高情况,抽测了某校17岁的50名男生的身高,将数据分成7组,列出了相应的频数分布表(部分未列出)如下:
某校50名17岁男生身高的频数分布表
请回答下列问题:
(1)请将上述频数分布表填写完整;
(2)估计这所学校17岁男生中,身高不低于1.655m且不高于1.715m的学生所占的百分比;
(3)该校17岁男生中,身高在哪个范围内的频数最多?如果该校17岁男生共有350名,那么在这个身高范围内的人数估计有多少人?
某校50名17岁男生身高的频数分布表
| 分 组(m) | 频数(名) | 频率 |
| 1.565~1.595 | 2 | 0.04 |
| 1.595~1.625 | 4 | 0.08 |
| 1.6254~1.655 | 6 | 0.12 |
| 1.655~1.685 | 11 | 0.22 |
| 1.685~1.715 | 17 | 0.34 |
| 1.715~1.745 | 6 | 0.12 |
| 1.745~1.775 | 4 | 0.08 |
| 合 计 | 50 | 1 |
(1)请将上述频数分布表填写完整;
(2)估计这所学校17岁男生中,身高不低于1.655m且不高于1.715m的学生所占的百分比;
(3)该校17岁男生中,身高在哪个范围内的频数最多?如果该校17岁男生共有350名,那么在这个身高范围内的人数估计有多少人?
 如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.