题目内容
 如图,在?ABCD中,AD=10cm,点E、F分别是BD,CD的中点,则EF=
如图,在?ABCD中,AD=10cm,点E、F分别是BD,CD的中点,则EF=考点:三角形中位线定理,平行四边形的性质
专题:
分析:根据平行四边形的对边相等可得BC=AD,再根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=
BC.
| 1 |
| 2 |
解答:解:在?ABCD中,BC=AD=10cm,
∵点E、F分别是BD,CD的中点,
∴EF是△BCD的中位线,
∴EF=
BC=
×10=5cm.
故答案为:5.
∵点E、F分别是BD,CD的中点,
∴EF是△BCD的中位线,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:5.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的对边相等的性质,熟记性质与定理是解题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
下列说法中正确的是( )
A、x-
| ||||
| B、x2-2x+25是五次三项式 | ||||
C、
| ||||
| D、x2y的系数为0,次数为3 |
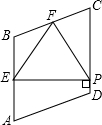 如图,在菱形ABCD中,∠A=80°,E、F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
如图,在菱形ABCD中,∠A=80°,E、F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )| A、40° | B、45° |
| C、50° | D、55° |
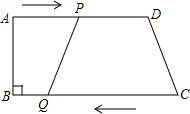 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿AD边以1cm/s的速度向点D运动,动点Q从C点开始沿CB边以3cm/s的速度向点B运动,P,Q分别从A,C同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.设运动的时间为t(s).
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿AD边以1cm/s的速度向点D运动,动点Q从C点开始沿CB边以3cm/s的速度向点B运动,P,Q分别从A,C同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.设运动的时间为t(s). 已知:如图,AB,CD为直线,DF交AB于E,EG交CD于O.若∠BEF=124°,∠D=56°,∠DEO=60°,则∠C0E的度数为
已知:如图,AB,CD为直线,DF交AB于E,EG交CD于O.若∠BEF=124°,∠D=56°,∠DEO=60°,则∠C0E的度数为 如图,已知正方形ABCD的面积为2,连接AC、BD,CE平分∠ACD交BD于点E,则DE=
如图,已知正方形ABCD的面积为2,连接AC、BD,CE平分∠ACD交BD于点E,则DE=