Question

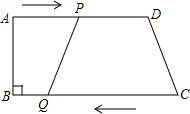如图，在四边形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P从A点开始沿AD边以1cm/s的速度向点D运动，动点Q从C点开始沿CB边以3cm/s的速度向点B运动，P，Q分别从A，C同时出发，当其中一个动点到达终点时，另一个动点也随之停止运动．设运动的时间为t（s）．
（1）当t为何值时，四边形ABQP是矩形；
（2）当t为何值时，四边形PQCD是平行四边形？
（3）问：四边形PQCD是否能成菱形？若能，求出运动时间；若不能，请说明理由．

Answer 1

考点：平行四边形的判定,矩形的判定

专题：动点型

分析：（1）由在梯形ABCD中，AD∥BC，∠B=90°，可得当AP=BQ时，四边形ABQP是矩形，即可得方程：t=26-2t，解此方程即可求得答案．
（2）由在梯形ABCD中，AD∥BC，可得当PD=CQ时，四边形PQCD是平行四边形，即可得方程：15-t=2t，解此方程即可求得答案；
（3）由若四边形PQCD是菱形，则四边形PQCD是平行四边形，根据（2）中的求解答案，分析看此时能否为菱形，因为CD≠PD，即可得四边形PQCD不可能是菱形；

解答：解：根据题意得：AP=tcm，CQ=3tcm，
∵AB=8cm，AD=24cm，BC=26cm，
∴DP=AD-AP=24-t（cm），BQ=26-3t（cm），
（1）∵在梯形ABCD中，AD∥BC，∠B=90°，
∴当AP=BQ时，四边形ABQP是矩形，
∴t=26-3t，
解得：t=6.5，
∴当t=6.5时，四边形ABQP是矩形；

（2）∵在梯形ABCD中，AD∥BC，
∴当PD=CQ时，四边形PQCD是平行四边形，
∴24-t=3t，
解得：t=6，
∴当t=6时，四边形PQCD是平行四边形；

（3）若四边形PQCD是菱形，则四边形PQCD是平行四边形，
根据（2）得：t=6s，
∴PD=24-t=24-6=18（cm），
过点D作DE⊥BC于E，
∴四边形ABED是矩形，
∴BE=AD=24cm，
∴EC=BC-BE=26-24=2（cm），DE=AB=8cm，
∴DC=

DE2+EC2

=2

17

≠PD，
∴四边形PQCD不可能是菱形；

点评：此题考查了直角梯形的性质、平行四边形的判定与性质以及矩形的判定与性质．此题难度适中，注意掌握数形结合思想与方程思想的应用．