题目内容
5. 如图,点C在⊙O的直径BA的延长线上,AB=2AC,CD切⊙O于点D,连接CD,OD.
如图,点C在⊙O的直径BA的延长线上,AB=2AC,CD切⊙O于点D,连接CD,OD.(1)求角C的正切值:
(2)若⊙O的半径r=2,求BD的长度.
分析 (1)根据CD切⊙O于点D,得出CD⊥OD,再根据AB=2CA,求出∠C=30°,即可得出答案;
(2)连接AD,证得△DAO是等边三角形,求出DA=r=2,再根据勾股定理可求得BD的长.
解答 解:(1)∵CD切⊙O于点D,
∴CD⊥OD,
又∵AB=2AC,
∴OD=AO=AC=$\frac{1}{2}$CO
∴∠C=30°
∴tan∠C=$\frac{\sqrt{3}}{3}$;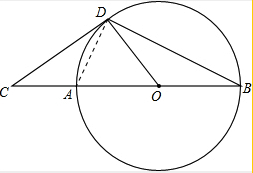 (2)连接AD,
(2)连接AD,
∵AB是直径,
∴∠ADB=90°,
∵∠DOA=90°-30°=60°,
又∵OD=OA,
∴△DAO是等边三角形.
∴DA=r=2,
∴DB=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
点评 此题考查了切线的性质,用到的知识点是切线的性质、三角函数的定义、勾股定理,关键是根据题意作出辅助线,得出直角三角形.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
16.小明解方程$\frac{2x-1}{3}=\frac{x+a}{2}$-1去分母时,方程右边的-1忘记乘6,因而求出的解为x=-2,那么原方程正确的解为( )
| A. | x=5 | B. | x=-7 | C. | x=-13 | D. | x=1 |
14.计算(-$\frac{1}{3}$)×3的结果是( )
| A. | -1 | B. | -2 | C. | 2 | D. | -$\frac{2}{3}$ |
15.党的十八届三中全会决定提出研究制定渐进式延迟退休年龄的政策,最近人社部新闻发言中心对延迟退休年龄进行了回应称:每年只会延长几个月.
渐进式退休年龄应该怎么算?《假定从2022年起实施延迟退休》
以55岁退休为标准,假定每年延长退休时间为6个月,自方案实施起,逐渐累计递增,直到达到新拟定的退休年龄,网友据此只做了一张“延迟退休对照表”.
(1)根据上表,1974年出生的人实际退休年龄将会是59岁;
(2)若每年延迟退休3个月,则2006年出生的人恰好是65岁退休.
渐进式退休年龄应该怎么算?《假定从2022年起实施延迟退休》
以55岁退休为标准,假定每年延长退休时间为6个月,自方案实施起,逐渐累计递增,直到达到新拟定的退休年龄,网友据此只做了一张“延迟退休对照表”.
| 出生年份 | 2022年年龄(岁) | 延迟退休时间(年) | 实际退休年龄(岁) |
| 1967 | 55 | 0.5 | 55.5 |
| 1968 | 54 | 1 | 56 |
| 1969 | 53 | 1.5 | 56.5 |
| 1970 | 52 | 2 | 57 |
| 1971 | 51 | 2.5 | 57.5 |
| 1972 | 50 | 3 | 58 |
| … | … | … | … |
(2)若每年延迟退休3个月,则2006年出生的人恰好是65岁退休.