题目内容
点C在线段AB上,M是AC的中点,N是BC的中点,若AC:CB=3:2,且MC+NB=12.5cm,求MC的长.
考点:两点间的距离
专题:
分析:根据线段中点的性质,可得AM=CM=
,CN=BN=
BC,根据线段的和差,可得MN的长根据等式的性质,可得AB的长,根据线段的比例,可得线段AC的长,再根据线段的中点,可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解;如图: ,
,
由M是AC的中点,N是BC的中点,得
AM=CM=
,CN=BN=
BC.
由线段的和差,得
MN=MC+CN=MC+NB=12.5(cm).
MN=MC+CN=
AC+
BC=
AB=12.5
AB=2MN=2×12.5=25(cm)
由AC:CB=3:2,得AC=3x(cm),BC=2x(cm).
AC+BC=3x+2x=25.
解得x=5,3x=15.
MC=
AC=
×15=7.5(cm).
 ,
,由M是AC的中点,N是BC的中点,得
AM=CM=
| 1 |
| 2 |
| 1 |
| 2 |
由线段的和差,得
MN=MC+CN=MC+NB=12.5(cm).
MN=MC+CN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
AB=2MN=2×12.5=25(cm)
由AC:CB=3:2,得AC=3x(cm),BC=2x(cm).
AC+BC=3x+2x=25.
解得x=5,3x=15.
MC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了两点间的距离,利用了线段中点的性质,线段的和差.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
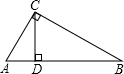 如图,在△ABC中,∠C=90°,CD⊥AB,D为垂足,求证:
如图,在△ABC中,∠C=90°,CD⊥AB,D为垂足,求证: 如图,将直角三角形顶点放在D(5,5)处,两直角边与坐标轴交点为E、F,则OE+OF的长是
如图,将直角三角形顶点放在D(5,5)处,两直角边与坐标轴交点为E、F,则OE+OF的长是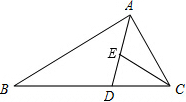 如图,在△ABC中,CD=CE,2AD=3AE,2BD=3CD,求证:△ABD∽△ACE.
如图,在△ABC中,CD=CE,2AD=3AE,2BD=3CD,求证:△ABD∽△ACE.