题目内容
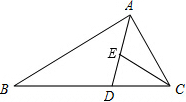如图，在△ABC中，CD=CE，2AD=3AE，2BD=3CD，求证：△ABD∽△ACE．考点：相似三角形的判定
专题：证明题
分析：根据等腰三角形的性质，由CD=CE得到∠CDE=∠CED，则利用邻补角的定义得到∠ADB=∠AEC，再根据比例的性质，由2AD=3AE，2BD=3CD得到
=
，接着用等线段代换得
=
，于是可根据两组对应边的比相等且夹角对应相等的两个三角形相似判断△ABD∽△ACE．
| AD |
| AE |
| BD |
| CD |
| AD |
| AE |
| BD |
| CE |
解答：证明：∵CD=CE，
∴∠CDE=∠CED，
∴∠ADB=∠AEC，
∵2AD=3AE，2BD=3CD，
∴
=
=
，
而CD=CE，
∴
=
，
∴△ABD∽△ACE．
∴∠CDE=∠CED，
∴∠ADB=∠AEC，
∵2AD=3AE，2BD=3CD，
∴
| AD |
| AE |
| BD |
| CD |
| 3 |
| 2 |
而CD=CE，
∴
| AD |
| AE |
| BD |
| CE |
∴△ABD∽△ACE．
点评：本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似．也考查了等腰三角形的性质．
练习册系列答案
阅读快车系列答案
相关题目
已知点A（-2，1），点B（3，2），在x轴上求一点P，使AP+BP最小，下列作法正确的是（ ）
| A、点P与O（0.0）重合 |
| B、连接AB交y轴于P，点P即为所求． |
| C、过点A作x轴的垂线，垂足为P，点P即为所求 |
| D、作点B关于x轴的对称点C，连接AC，交x轴于P，点P即为所求 |
如图，已知正方形ABCD与正方形CEFG，点G在边CD上，连接AF，取AF中点M，连接DM、GM．求证：
如图△ABC中，AB=BC，BC⊥AC于点E，AD⊥BC于点D，∠BAD=45°，AD与BE相交于点F，连接CF．
有一条长12m的木料做成如图的日字形窗框，请你计算出窗框的宽和高各取多少m时，这个窗框面积S最大．